Monkey Saddle Surface

by Tuğrul Yazar | April 8, 2012 22:18

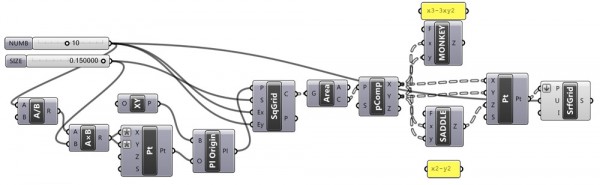
This is another popular “math surface” being rediscovered by designers nowadays, in 2012. Saddle surfaces, seen above as mentioned earlier (here) have a special type named “Monkey Saddle Surface”. This surface was a dramatic example of how Grasshopper can control equations and instantly show graphical results. The mathematical equations start with Z=… this makes it very easy for us to transform any x-y grid centers (a 2d data tree of 3d points) and add z values to them according to that equation. Monkey Saddle’s center point (0,0,0) is the only point with zero curvature. All other coordinates have negative curvature. This surface looks interesting when I animate it as shown below:

Interestingly, this surface is a similar (and idealized) version of my hand-made test surfaces for Grasshopper experiments. Maybe I’ll use this one to test GH definitions from now on. Please be aware that this definition draws both surfaces at the origin of Rhino space, which is tiny. So don’t forget to zoom in. It’s fun to play with. In fact, the definition is capable of generating any equation surface, other than the famous Monkey Saddle Surface. For example, here is what happens when I enter cos(x2+y2)*0.33 into the function;

You can re-create the Grasshopper definition by checking the diagram above. However, if you liked this content and want to support me by downloading the Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page [2]including the working Grasshopper file for the Monkey Saddle Surface and more.

Source URL: https://www.designcoding.net/monkey-saddle-surface/

---