Moebius Transformation

by Tuğrul Yazar | July 5, 2012 14:07

[GHX: 0.8.0066][1] This is my second attempt on getting into non-euclidean representations of space. Althouth it seems easy at first sight, this represents a close point of theory between mathematics and contemporary computational design geometry. As always, architects tend to use mathematical terms such as “non-euclidean geometries” but as far as I saw, most of them have no idea about what it is. So, I’m trying to learn and understand this connection by experiencing small parts of it, sailing at the edges of architectural geometry, but trying not to get into equations of mathematics.

There are diverse approaches to study spherical and hyperbolic geometries but there seem to be no clear and easy equation that maps an Euclidean space into a non-Euclidean one, unless we are not dealing with the real projective way of describing them. My initial experiment was to understand the transformation between Cartesian coordinates and a projective transformation such as Moebius transformation. There is a beautiful video called “a video worth thousand words” at youtube (here)[2] showing this process. While I was trying to get into the equations of these conversions from Cartesian to Hyperbolic space, that visual explanation changed my orientation back to the designerly way.

Below is my first attempt to describe a regular square tessellation using stereographic projection. The sphere used here is named Riemann sphere, there is a whole branch of mathematics about that.

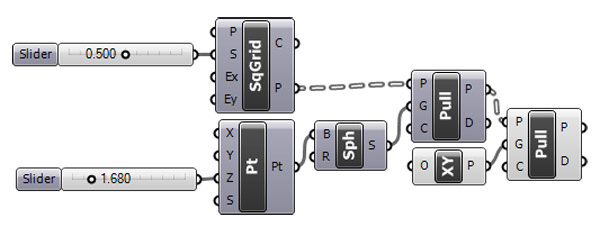
As you see, this is very effective and easy in Grasshopper for now. But getting into deeper areas of tessellations might be further interesting and complex. I’ll get more into this ASAP.

Source URL: https://www.designcoding.net/moebius-transformation/

---