Modeling The Gyroid

by Tuğrul Yazar | May 16, 2023 23:24

Here is the method I used for approximately modeling the Gyroid[1], a triply-periodic minimal surface. It is very popular in architecture because the symmetrical solids and voids it generates are interesting. I modeled this for the Common-action Wall[2] project we exhibited together with Fulya Akipek in 2017. After several attempts to generate it in Grasshopper, I decided to model it in Rhino. There are some sources on the internet, explaining the geometric modeling process. However, none of them was giving me the continuous, smooth Gyroid (as far as I searched). So, here is my modeling process step-by-step;

The important point is to define the fundamental curve which will provide us with a good approximation. After a short search, I found that the implicit function of the Gyroid surface is:

Cos(x) * Sin(y) + Cos(y) * Sin(z) + Cos(z) * Sin(x) = 0

Thus, the fundamental curve of the Gyroid can be described in the parametric form as;

x = ArcSin (Sin(t) / Cos(t)), y = 0, z = t, while 0 ≤ t ≤ π/4.

I used below Rhino Python script to draw the fundamental curve using the function above:

import rhinoscriptsyntax as rs
from math import *
points = []
t = 0
while t <= pi/4:
	x = asin(sin(t)/cos(t))
	points.append([x,0,t])
	t = t + 0.02
x = asin(sin(pi/4)/cos(pi/4))
points.append([x,0,pi/4])
rs.AddInterpCurve(points)

After drawing it, I rotate and copy it to achieve the below edges. Then, I use the Patch command to create the fundamental patch.

Then, I rotate and copy the fundamental patch to achieve the below piece:

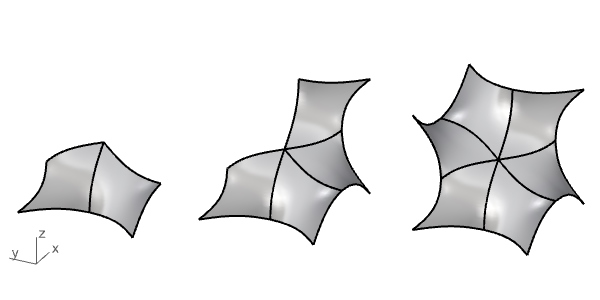
Finally, once again, I copy and rotate the piece to create the Gyroid surface:

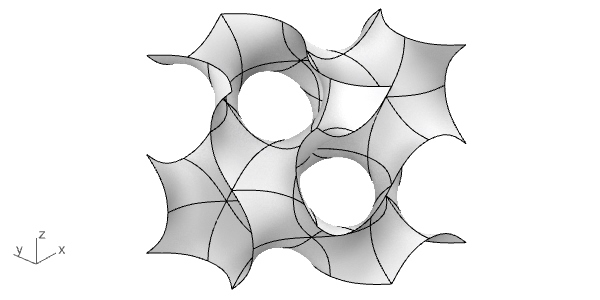
You can rebuild the model with the explanation above. However, if you want to support this website by downloading my Rhino file; would you consider being my Patreon? Here is the link to my Patreon page[3] including the Modeling the Gyroid and more.

Source URL: https://www.designcoding.net/modeling-the-gyroid/