An octahedron is a three-dimensional polyhedron with eight triangular faces, six vertices, and twelve edges. It is one of the Platonic solids and has high symmetry, with all of its faces being equilateral triangles. A regular octahedron can be visualized as two pyramids joined at their bases. It has the same number of faces as a cube has vertices, and the same number of vertices as a cube has faces. The octahedron is also dual to the cube, meaning that the vertices of a cube correspond to the faces of an octahedron, and vice versa. In this short tutorial video, I am modeling and unrolling an octahedron by using the Euclidean approach. I studied this construction earlier here.

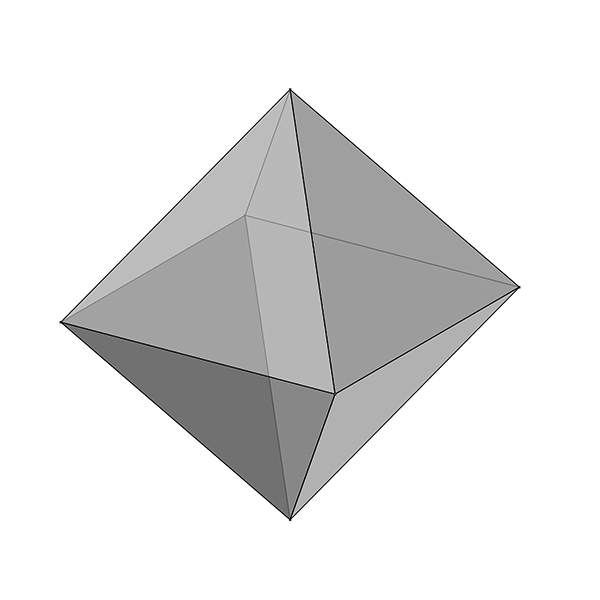
In this video series, I present a variety of in-class exercises from my first-year Architectural Geometry course. Using Rhinoceros software, we delve into Euclidean constructions, basic drawing and transformation commands, introductory fractals, regular and semi-regular tessellations, patterns, modeling, and unrolling polyhedra. Also, these concise drawing exercises are beneficial for junior architects, interior designers, industrial designers, and enthusiasts from other disciplines. I’ll be sharing exercises each week on my blog and other platforms. So, today’s exercise is modeling and unrolling octahedron.

The software used in this course is Rhinoceros 3d (www.rhino3d.com). However, if you want to find out more and see the whole list of this video series, you can check my YouTube channel at www.youtube.com/@designcodingnet and my blog at: www.designcoding.net/. You can also check my Instagram page at www.instagram.com/designcodingnet/. The music of this video is ‘Life in Silico’ by Scott Buckley (CC-BY 4.0). www.scottbuckley.com.au