Modeling and Unrolling Dodecahedron

by Tuğrul Yazar | December 12, 2024 09:20

A dodecahedron is a three-dimensional polyhedron[1] with twelve flat, regular pentagonal faces, twenty vertices, and thirty edges. It is one of the Platonic solids[2] and is highly symmetrical, with each face being a regular pentagon. The dodecahedron’s shape is unique among the Platonic solids because its faces are polygons with five sides, unlike the others which have triangular faces. Due to its symmetry, the dodecahedron has been used in various applications, including as a model in geometry and in certain dice used in role-playing games. In this short tutorial, I am modeling and unrolling a dodecahedron in Rhinoceros software. In this process, I utilize sphere intersections to locate vertices. The key point of the tutorial is to determine the inner angles of the polyhedron by using spheres. I studied this beautiful solid here[3], here[4], and here[5] before.

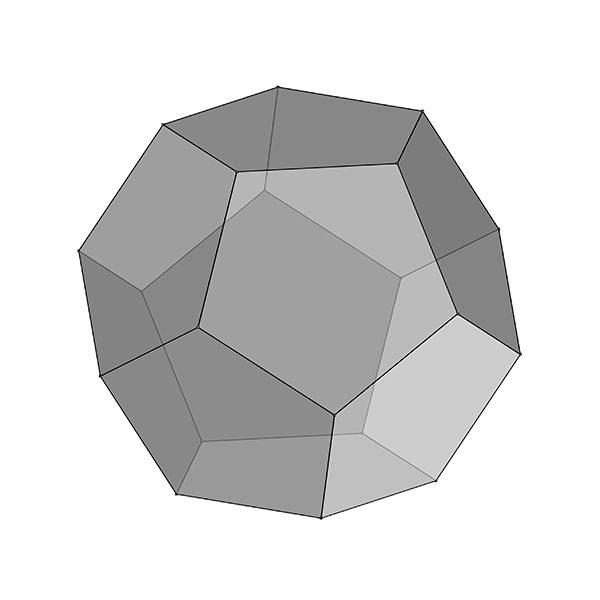
I have been conducting a series of in-class exercises in the freshmen year Architectural Geometry course, focusing on Euclidean constructions[6], basic drawing and transformation commands, introductory fractals[7], regular and semi-regular tessellations[8], patterns[9], modeling, and unrolling polyhedra[10] using Rhinoceros[11] software. Junior architects, interior designers, industrial designers, and enthusiasts from other disciplines can benefit from these concise drawing exercises. I will publish exercises every week on my blog and other platforms. So, here is today’s exercise; modeling and unrolling dodecahedron.

The software used in this course is Rhinoceros 3d (www.rhino3d.com[12]). However, if you want to find out more and see the whole list of this video series, you can check my YouTube channel at www.youtube.com/@designcodingnet[13] and my blog at: www.designcoding.net/[14]. You can also check my Instagram page at www.instagram.com/designcodingnet/[15]. The music of this video is ‘Celestial’ by Scott Buckley (CC-BY 4.0). www.scottbuckley.com.au[16]

Source URL: https://www.designcoding.net/modeling-and-unrolling-dodecahedron/

---