Modeling an Icosahedron

by Tuğrul Yazar | December 21, 2011 01:12

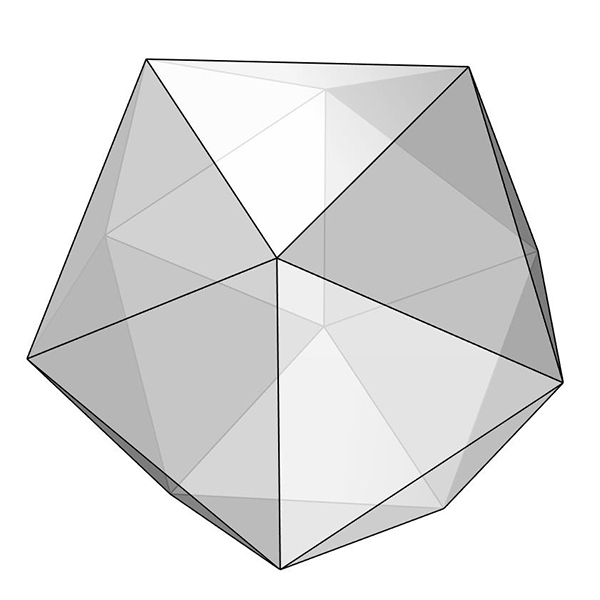
Today’s polyhedra[1] is the beautiful icosahedron[2]. It is one of the five Platonic Solids[3] with twenty equilateral triangular faces. Its dual is the dodecahedron[4], which has pentagonal faces. Here, I explained the process of modeling an icosahedron. After creating a regular pentagon, you should find the “tip” point of the Icosahedron by intersecting spheres from at least three of the corner points with a radius of the pentagon’s edges. You can exercise Tetrahedron to understand how we find a point in three dimensions. It lies at a certain equal distance from three other points. The trick here is to 3d rotate and copy the pentagon to construct the inner angle of the solid. Then, it’s easy to repeat the process to complete the object by creating all 20 triangular faces and joining them into a single object.

This tutorial creates a Rhino file (3dm Rhino 7 format) including one closed polysurface object. Therefore, it is ready for unrolling flat, or 3d printing without problem. You can use this model to further investigate the archimedean solid of truncated icosahedron (buckyballs), and the famous geodesic spheres. Thus, this solid creates the foundation of many other interesting objects.

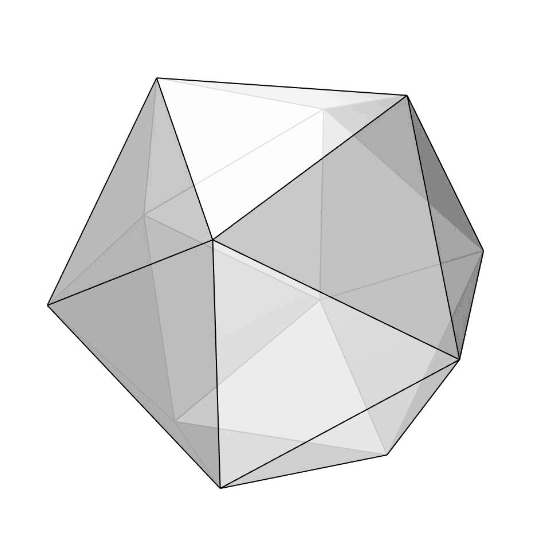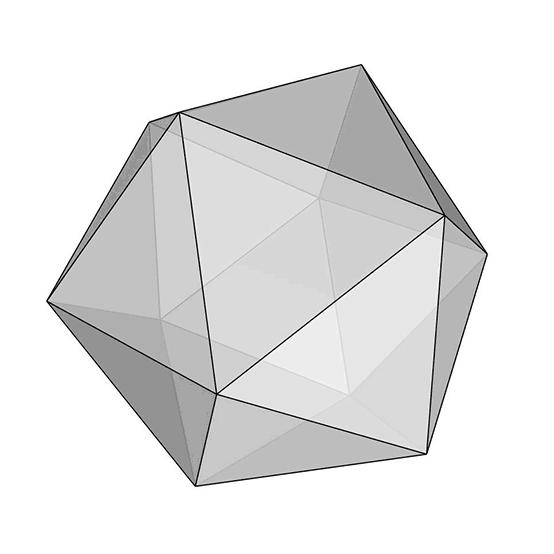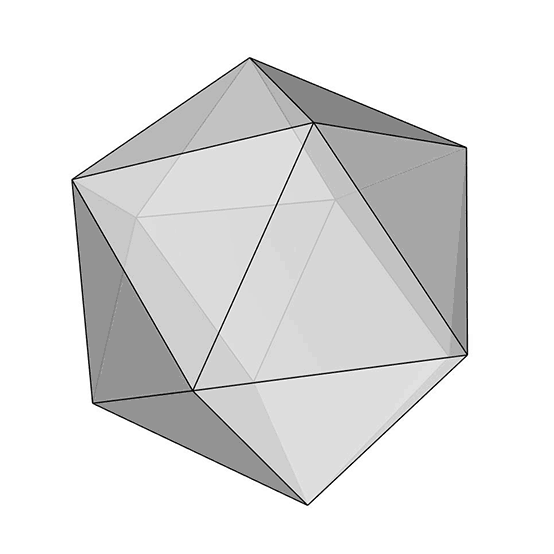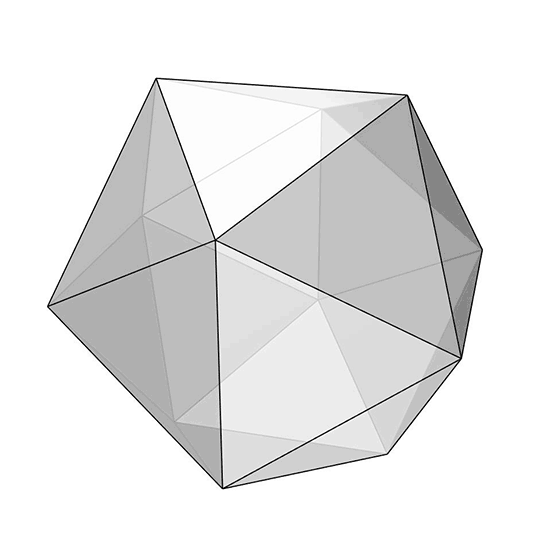
You can re-build the model by watching the tutorial video seen above. However, would you consider being my Patreon if you liked this content and want to support this website? So that you can download my Rhino file for icosahedron. Here is the link to my Patreon page[5] including the Rhino file for the modeling of an icosahedron and more.

Source URL: https://www.designcoding.net/modeling-an-icosahedron/

---