This is the updated version of my MST code from 2012. After over a hundred hours of Rhinocommon and Grasshopper SDK studies, and lots of dead ends, I was finally able to calculate the minimum spanning tree of any given curve network in Grasshopper. Problems like these are interesting to me because of their clear logic and diverse areas of applications in design. I tried to simulate Dijkstra’s, Kruskal’s, and Prim’s algorithms, but no chance. There are similar solutions such as Shortest Walk and SpiderWeb which are much more faster and professional than mine. I chose a reverse-delete algorithm. The logic is simple: take the longest connection in the set. Then, see if you delete the connection, and whether the two nodes are still connected or not. If deleting that connection does not remove the two nodes, then delete it and continue from the next longest connection.

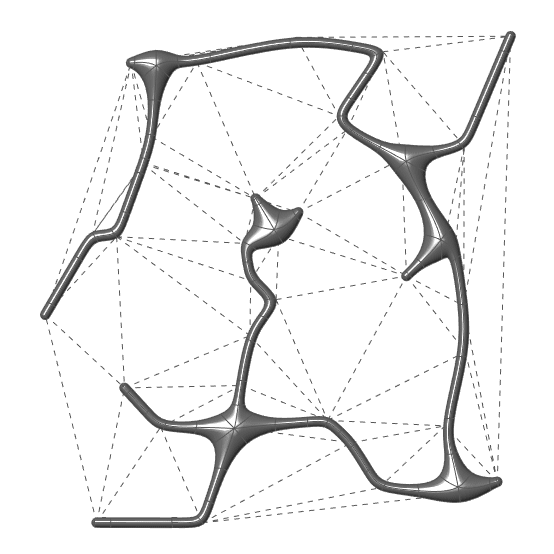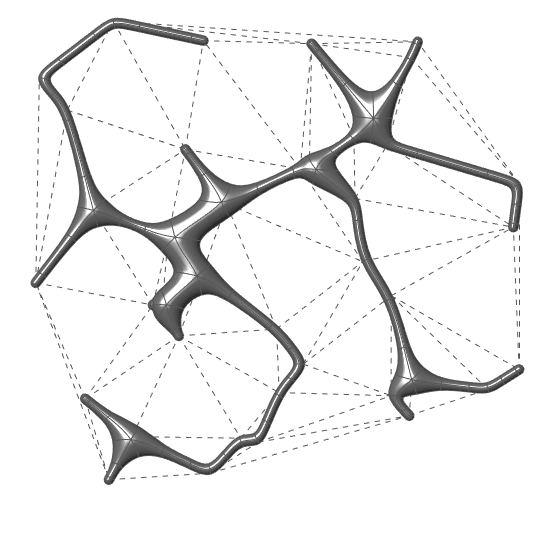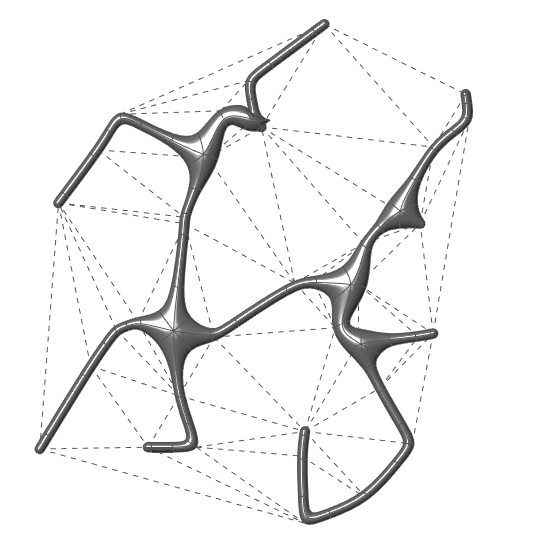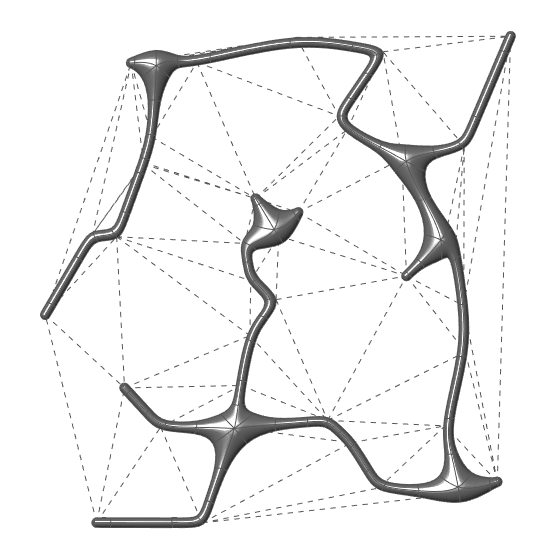
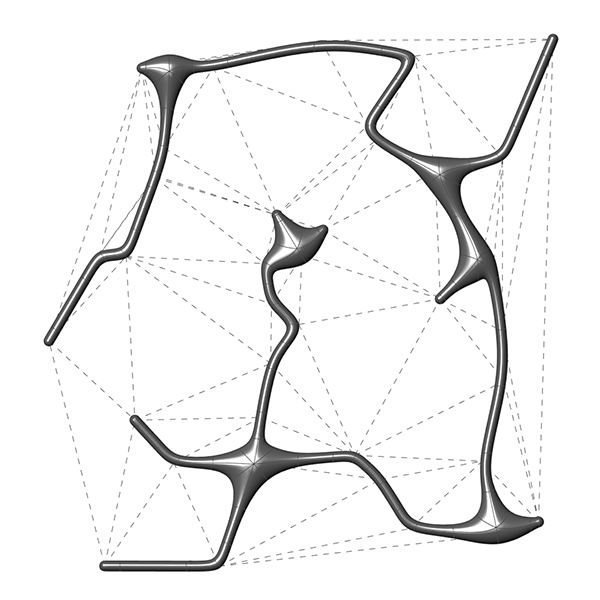
This Grasshopper definition includes one component written in VB.net language and it generates the Minimum Spanning Tree of a given curve network (a list of connected lines) in 2D and 3D. I added a standard Delaunay Triangulation to test it in the Grasshopper definition. The only input of the code is the list of lines. The outputs are the minimum spanning tree as line objects, and the step-by-step explanation texts of the operation. The code is using native Grasshopper components. Thus, no add-ons are necessary for it to work. This animation visualizes the outcome with a MultiPipe.

If you liked this content want to use it in your project, or want to study the Vb.net code, would you consider being my Patreon? Here is the link to my Patreon page, including the Minimum Spanning Tree files and more. Thank you for your support!