Minimal Parquet Deformations
by Tuğrul Yazar | January 28, 2013 00:08
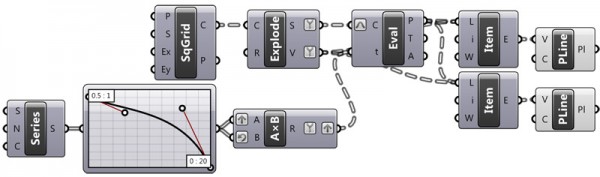
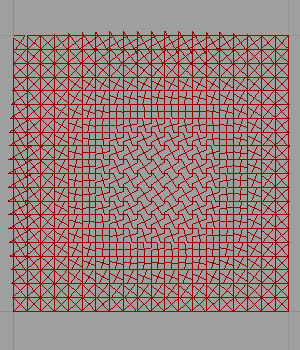
Is it possible to model a two-way parquet deformation[1] using only native components of Grasshopper? In this definition, I limited myself to 10 of them. Parquet deformations[2] are a very interesting and pedagogical topic to teach some of the basics of contemporary parametric modeling. This post explains a minimal parquet deformations algorithm in Grasshopper. However, this has its own limitations. You will see that the definition generates the attractor graph curve. Because the graph input tool creates the magic here. If you change the type of graph you’ll see a sort of representation over a simple pattern deformation based on rotating X’s.
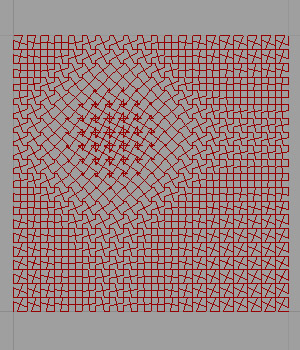
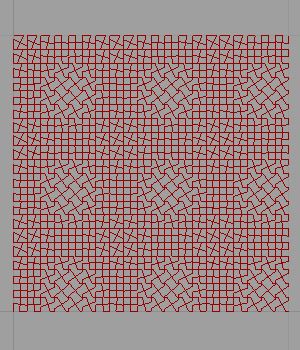
 [3]
[3]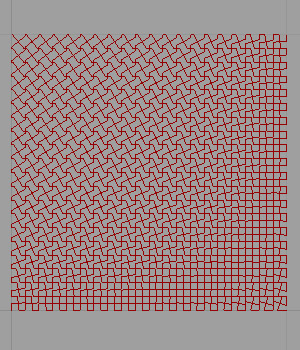
Here is the Grasshopper definition:
It is becoming a significant research topic to introduce students of architecture to systems thinking in the form of patterns and their deformations. Therefore, the Parquet Deformation exercise is about the tessellations of the plane that gradually shapeshift in two dimensions. We must do this without gaps or overlaps. The exercise encourages students of architecture to think about the geometric relationships between the sequences of continual shape-shifting while developing reasoning about a pattern as a structural whole. This is expected to be explored by morphing the cells of a pattern while sustaining its visual continuity and rhythm. This study is a continuation of the previous study on the reconstruction of parquet deformations via contemporary parametric modeling tools. Minimal parquet deformations Grasshopper algorithm can be further studied into a set of custom components. Thus, maybe an add-on in the future. I hope that one day, I can do that.
- parquet deformation: http://www.tess-elation.co.uk/parquet-deformations
- Parquet deformations: https://www.designcoding.net/category/research/pattern-deformations/
- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2013/01/2013_01_27-parq-th.jpg
- Download: https://www.designcoding.net/decoder/wp-content/uploads/2013/01/2013_01_27-parquet.ghx
Source URL: https://www.designcoding.net/minimal-parquet-deformations/