Lissajous curves, named after the French physicist Jules Antoine Lissajous are a family of curves that emerge from the interaction between two harmonic oscillations. They have applications in various fields including physics, engineering, and signal processing. They are commonly used in electronic devices such as oscilloscopes to visualize the phase relationship between two oscillating signals. Similarly, they are also useful in mechanical engineering for analyzing and designing mechanisms that involve harmonic motion. Lissajous curve functions can help in understanding the behavior of vibrating systems, such as pendulums, springs, and rotating machinery. Beyond their technical applications, Lissajous curves are easy to code and incorporate into various art forms and designs. I tried to implement a Lissajous Pendants design by utilizing and deforming the original curve function. This code can generate many different and interesting variations. You can see one of them in this animation.

This Grasshopper definition generates Lissajous curves and their improvizations with several input parameters. The f(t) and g(t) functions, density, parameter, and all variables of a standard Lissajous curve are the user-controlled inputs. You can generate original Lissajous curves and several deformed variations of them by playing with the inputs. The outputs are polysurfaces (pipe objects) and the NURBS curve. Therefore, it is possible to 3d print the output. I made the definition with the help of the native Grasshopper components in Rhinoceros 7. So, you don’t need to install any add-on to be able to use the definition.

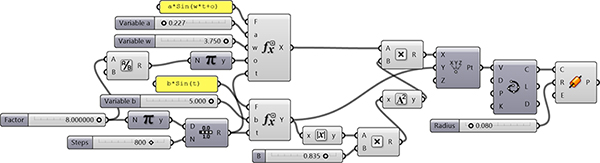
You can rebuild the definition by looking at the diagram above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? The link to my Patreon page includes the working Grasshopper file for the Lissajous Pendants and more.