Islamic Patterns of Semi-Regular Tessellations

by Tuğrul Yazar | October 22, 2012 13:15

The intricate harmony of the Islamic Patterns is amazing. The geometry of this and other Islamic pattern designs are explained in the 3rd chapter[1] of Craig S. Kaplan’s Ph.D. dissertation. I constructed a semi-regular tessellation[2], particularly the 4.8 because it seems to open interesting explorations that mostly emerge from truncated squares. We know equilateral triangles and hexagons are also fundamental shapes for this task. However, the dual nature of the semi-regular tessellations makes a difference in most compositions. First, I focused on developing a truncated square tiling. It was easy to divide and rebuild the grid cells in octagons. However, it was also necessary to tell Grasshopper that there are emergent small squares. The rest was easy, offset the square and octagon, then re-build with the proper vertex IDs. Overall, it is a good exercise for pattern studies in Grasshopper.

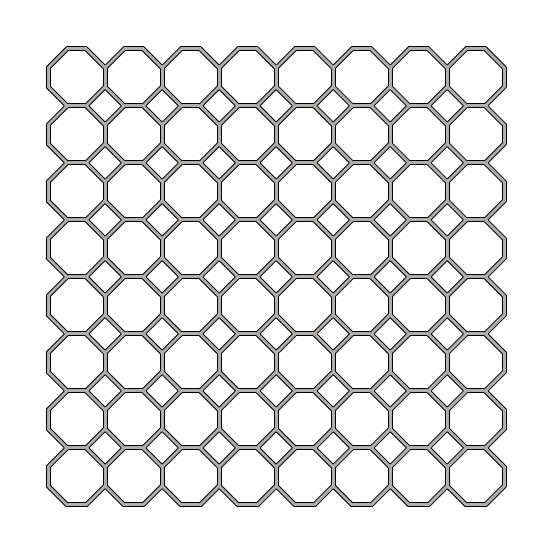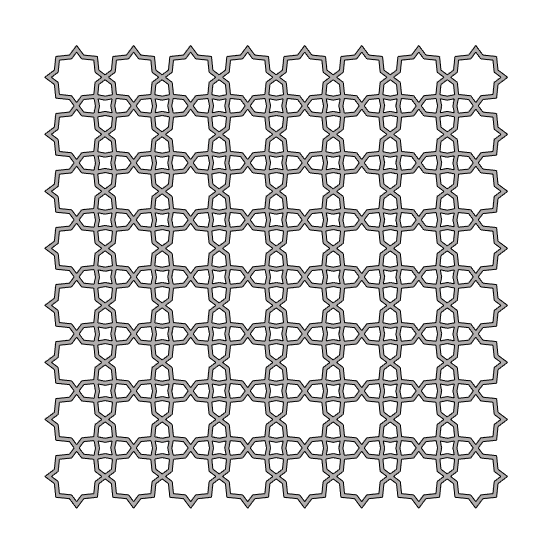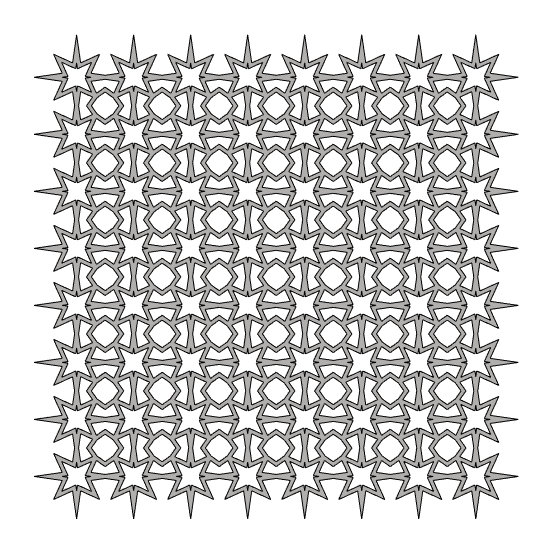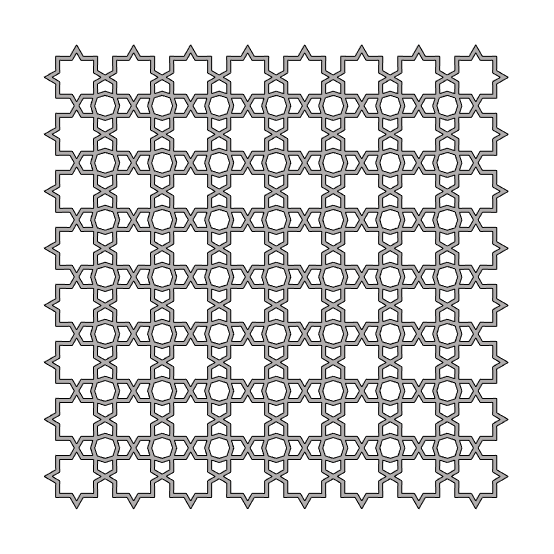
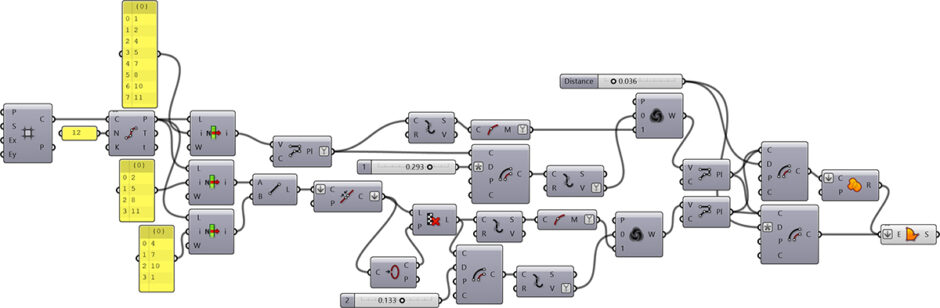
This Grasshopper definition generates Islamic Patterns based on the semi-regular tessellation of 4.8. The input parameters are the number of the grid cells, the parameters of both octagonal and quadrangular stars, and the offset value of the lattice. The code is using native Grasshopper components. Thus, no add-ons are necessary for it to work. However, you can implement the Clipper add-on for faster lattice calculation.

You can rebuild the Grasshopper definition by looking at the image above. However, would you consider being my Patreon if you want to support this website by downloading my working file? Here is the link to my Patreon page[4], including the Islamic Patterns of Semi-Regular Tessellations and more. Thank you.

Source URL: https://www.designcoding.net/islamic-patterns-of-semi-regular-tessellations/

---