Inverse Kinematics in Rhino Python

by Tuğrul Yazar | May 22, 2019 11:05

This is a simple inverse kinematics solution developed by Andreas Aristidou and Joan Lasenby in 2011. They call it Forwards and Backwards Reaching Inverse Kinematics (FABRIK[1] in short). It was quite interesting the learn this technique because it is a fast and accurate approximation of a kinematic chain. There are very interesting potentials of this technique in terms of architectural simulations. I tried to develop a Rhino Python script in Rhino 6. It seems to be working properly. Here is the simple explanation of the FABRIK method:

The Process of FABRIK’s Inverse Kinematics

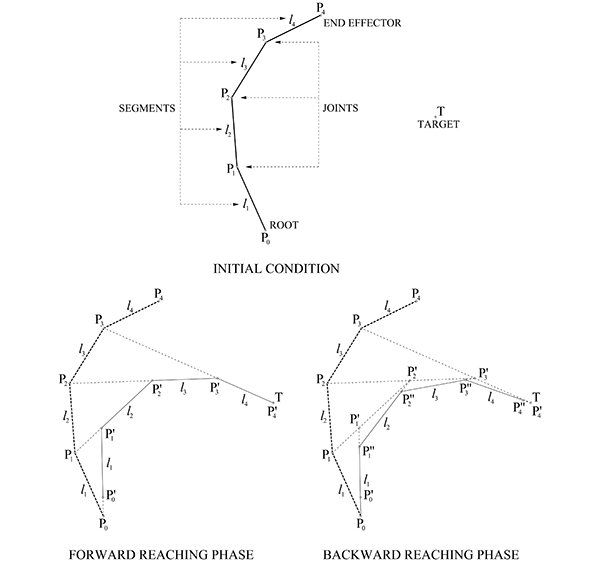
The algorithm of FABRIK requires geometers to define an initial condition. We will use an arbitrary set of joints, root, an end-effector, and a target point to explain the process. The algorithm has two major phases; a forward phase, and a backward phase. These phases include iterative modification of the joints. The forward phase starts at the end effector of the chain and works forwards, adjusting each joint one by one. Pn is relocated on T, redrawing the link ln between Pn and Pn-1, while keeping the length of this link unchanged. This phase finishes by relocating all vertices including the root, P0 temporarily defining P′0.

After the first phase, the algorithm works backward in the same way, relocating P′0 to P0 back again. These two phases complete one full iteration. After every iteration, the end-effector Pn gets closer to T. The iteration stops when the end-effector reaches the target position, or the error is sufficiently small. Notice that there can be conditions in which it is not possible to reach a perfect solution.

The Code in Rhino Python

First, the script asks a user some basic setup information such as the number of joints and their 2d locations on the plane. The last joint is regarded as the end-effector similar to the concept in robotics[2]. Then, the user enters a goal point. The script calculates the rotations of the joints to reach the goal point. The user can control the accuracy of the solution. However, in the current version, the script gives up after 10 iterations because in some cases it would be impossible for the manipulator to reach the goal point.

Here is the code if you want to try:

import rhinoscriptsyntax as rs
joints = []
legs = []
legsl = []
jNr = rs.GetInteger("Enter the number of joints:",4,2,8)
for i in range(0, jNr): 
	joints.append(rs.GetPoint("Locate joint nr."+str(i)))
rs.AddPoints(joints)
goal = rs.GetPoint("Locate the goal")
rs.AddPoint(goal)
precision = rs.GetReal("Enter the precision:",0.1,0.001,1)
arm = rs.AddPolyline(joints)
base = joints[0]
legsl = rs.ExplodeCurves(arm, True)
for l in legsl: legs.append(rs.CurveLength(l))
joints.insert(jNr, goal)
legs.append(0)
error = rs.Distance(goal, joints[jNr-1])
def chain(ch, lh, i):
	while i > 0:
		temp1 = rs.AddLine(ch[i], ch[i-1])
		if lh[i-1] > 0: temp2 = rs.EvaluateCurve(temp1, lh[i-1])
		if lh[i-1] == 0: temp2 = ch[i]
		ch[i-1] = temp2
		rs.DeleteObject(temp1)
		i = i - 1
	return ch
iteration = 0
while error > precision:
	chain(joints, legs, jNr)
	del joints[jNr]
	joints.reverse()
	joints.insert(jNr, base)
	del legs[jNr-1]
	legs.reverse()
	legs.insert(jNr-1,0)
	chain(joints, legs, jNr)
	rs.AddPolyline(joints)
	del joints[jNr]
	joints.reverse()
	joints.insert(jNr, goal)
	del legs[jNr-1]
	legs.reverse()
	legs.insert(jNr-1,0)
	error = rs.Distance(goal, joints[jNr-1])
	iteration = iteration + 1
	print "iteration #"+str(iteration)+": Error="+str(error)
	if iteration > 10: break  # Safety exit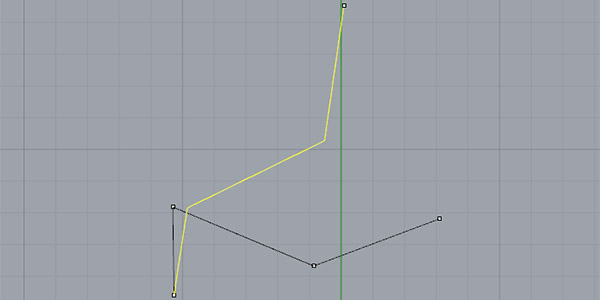

I loved the elegance, accuracy, and simplicity of this method. I would like to try to improve this code and develop 3d calculations and multiple end-effector and multiple-base versions.

Source URL: https://www.designcoding.net/inverse-kinematics-with-rhino-python/