Inflating Grids

by Tuğrul Yazar | December 28, 2012 11:05

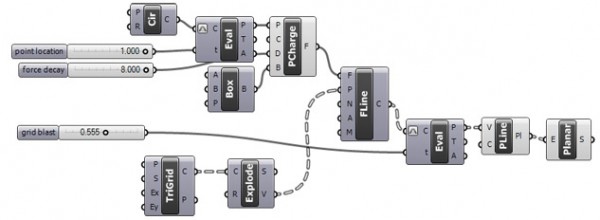
After playing with vector fields in 2d (here) it was quite easy to create a 3d surface deformation. Here is my first experiment on a regular triangular grid’s three-dimensional behavior within a vector space, that includes a point charge of varying z coordinates. That makes field lines escape to a bounding box, instead of a bounding rectangle. Again, you may play with force decay, the number of samples, and the “grid blast” parameter, which is just a t-value evaluation of force fields. The first animation below shows the traveling point with constant decay and charge values, while the second one shows a static point an increasing charge value. Note that field lines on every vertex escape to the boundary of the field. So the object affected by the vector field tends to get the shape of a bounding box at the end.

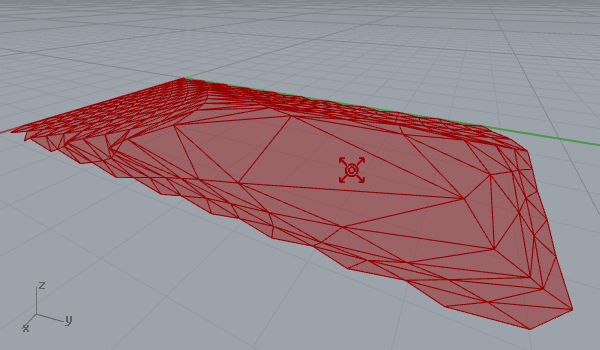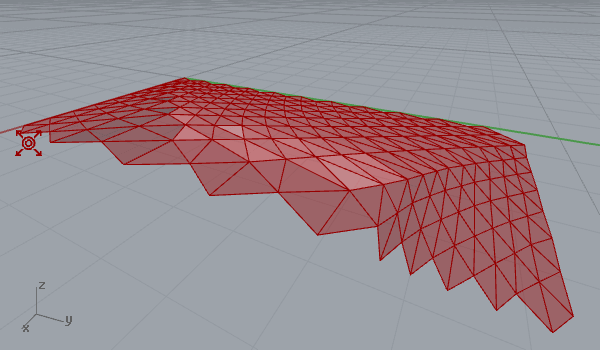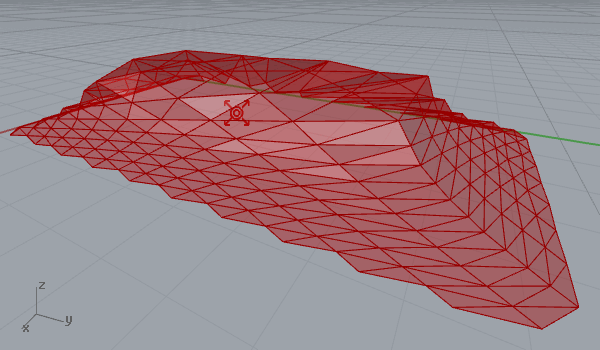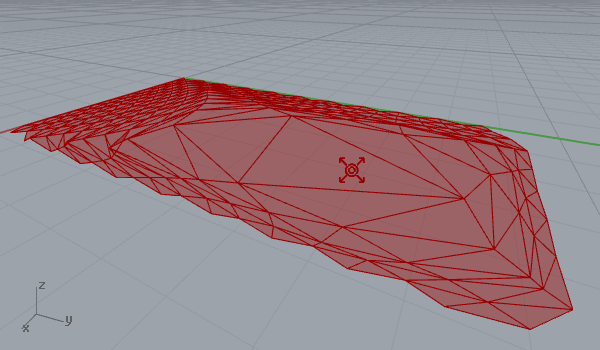
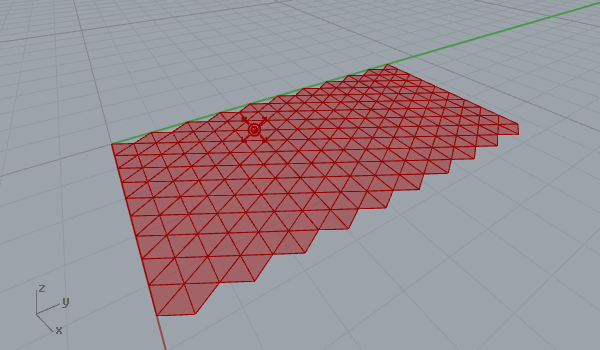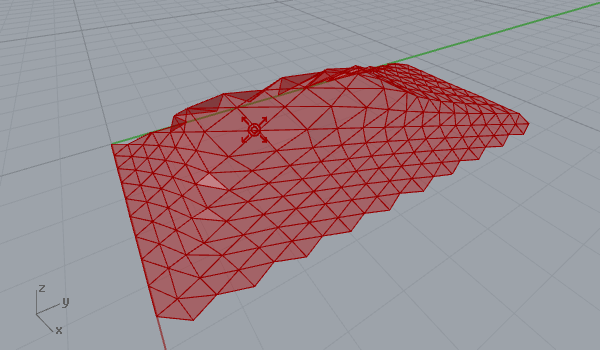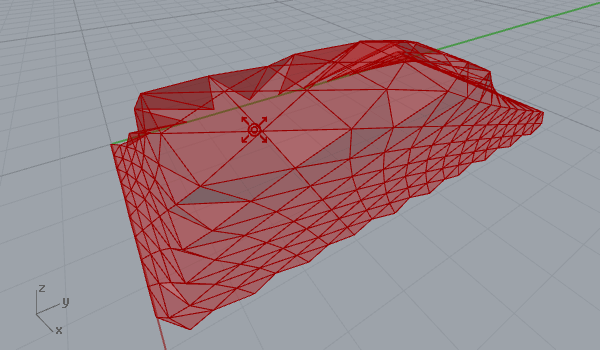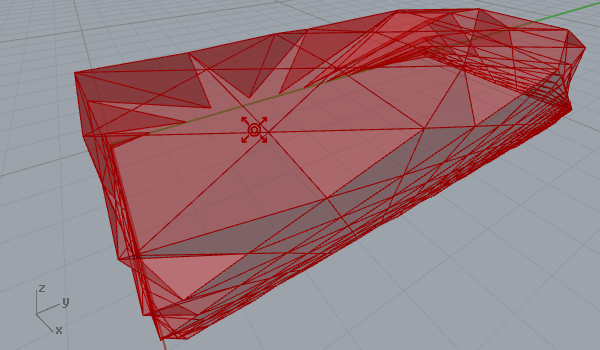
[1]

Yes, it is that easy and exciting with force fields. Here is the Grasshopper definition: [GHX: 0.9.0014][2]

Source URL: https://www.designcoding.net/inflating-grids/

---