Icosidodecahedron

by Tuğrul Yazar | December 22, 2011 01:59

Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from Icosahedron below;

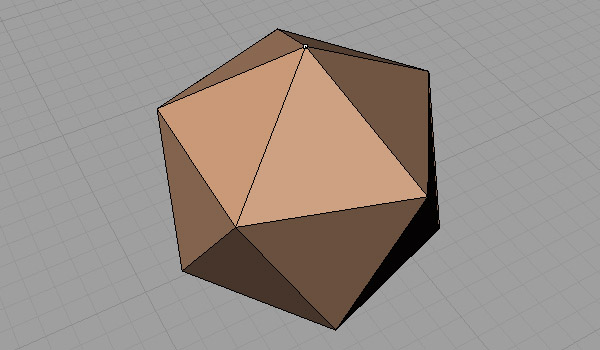
First, you should create an Icosahedron, the Platonic father of Icosidodecaheron. After that, all faces should be joined together to form a polysurface.

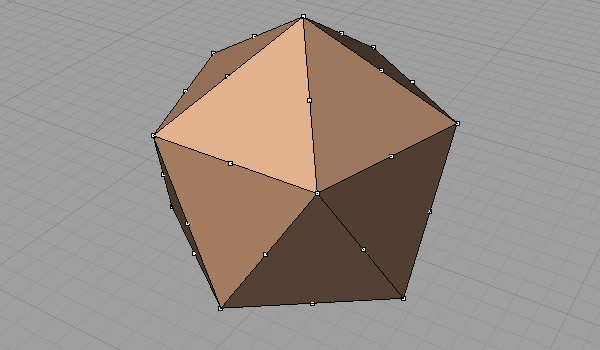
Then, extract all of its edges, using (Curve/Curve from Objects/Duplicate Edge) and divide them into two equal segments, using the (Curve/Point Object/Divide Curve by/Number of Segments/) command.

Now, the points should construct the faces of the Archimedian Solid.

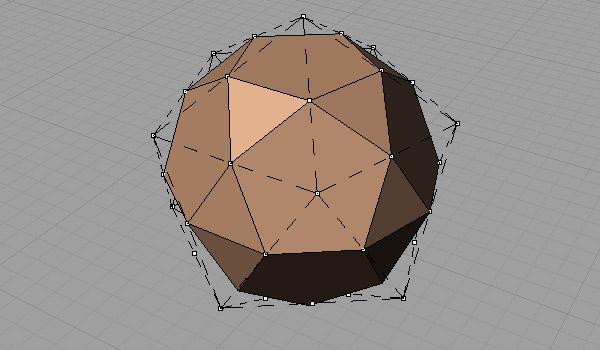
Here is the result.

Source URL: https://www.designcoding.net/icosidodecahedron/

---