Icosahedron Study

by Tuğrul Yazar | May 27, 2012 13:23

I have come across several high school topics I was afraid of. While I was searching for a geodesic dome definition in Grasshopper, it was quite surprising that I found an easier way of modeling an approximation of icosahedron, the famous platonic solid. Icosahedron was a research topic of this website at various posts before (here, here, and here). In order to generate geodesic spheres, first I had to solve icosahedron. My first experiment was partially successful. I knew icosahedron’s points lie at regular pentagons which are pulled onto a sphere.

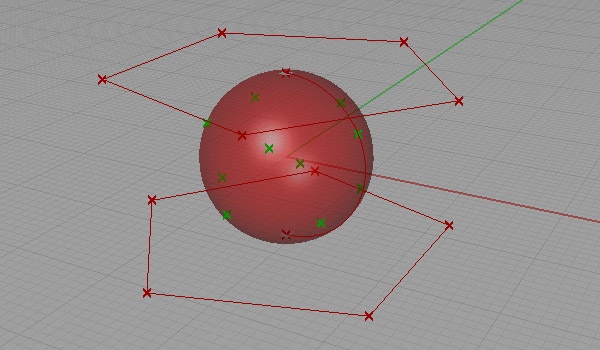
It sounds simple, but it is not. The radius of the planar pentagon to be pulled on the sphere should have a geometric relationship with the sphere radius or the desired edge length of the icosahedron. I found various formulas that represent the relationship between the icosahedron’s sphere radius and edge length. Unfortunately, they are not equal. If we call the radius of the sphere r, and the edge length of the icosahedron as a, here is their formula;

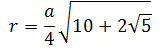or approximately saying, r = a * 0.9510565162…

However, this does not solve my problem either. I needed to find the radius of the pentagon. I’m sure it is a simple question for a math expert, but as I was not good at math in high school, I realized that I’ll never be.

As I couldn’t manage to find or develop an equation, I measured using a unit sphere and found a ratio of 1.90210898. That worked. Here is the Grasshopper definition that uses a pull component to create an equally divided icosahedron on a sphere [GHX: 0.8.0066]. Although it is the quite a short and efficient definition, it became boring at this stage and I quit this method without constructing icosahedron faces, or a geodesic sphere.

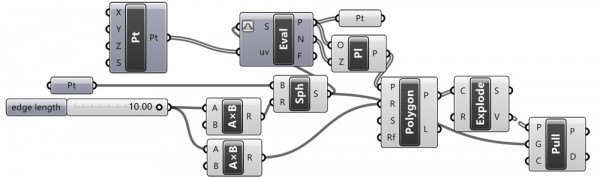[1]

My next try was about another phenomenon of math, which I knew from both high school and the school of architecture. I was completely sure about not using that ancient order in my designs. Yesterday, I used it. The golden ratio was an interesting one (represented by a symbol, phi; equals approximately 1.618034…) for designers and mathematicians because of its connection to nature, physics, and human perception. There is an alternative method of icosahedron construction that uses three golden ratio rectangles, which lie at the same origin but are rotated on different planes. It was simple to model that approach. Here is the definition: [GHX: 0.8.0066][2] This time, I created icosahedron faces also.

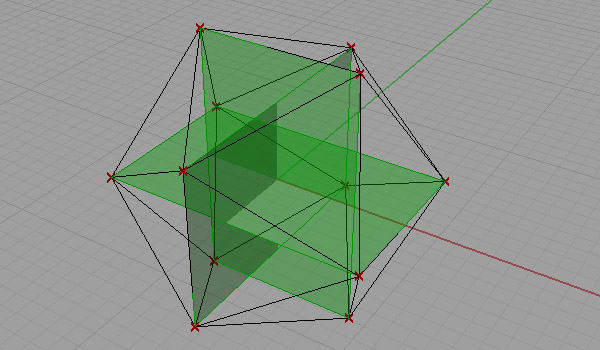
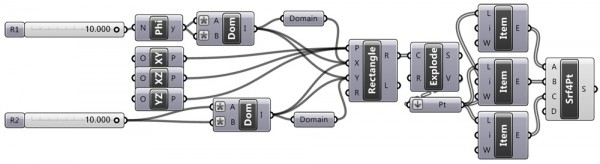[3]

As you see from the definition, I omitted the two radius sliders that create the rectangles. When I animated these values separately, result was very surprising to me;

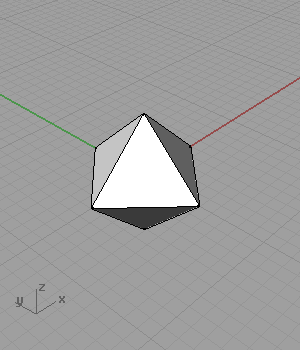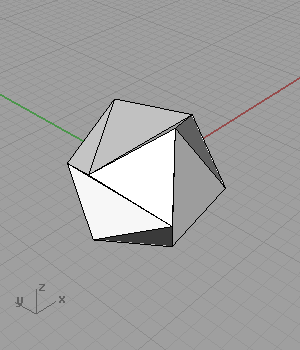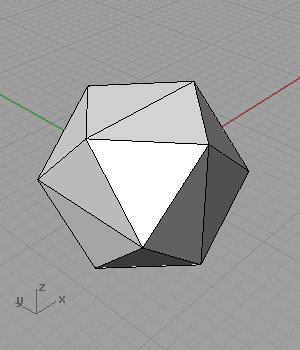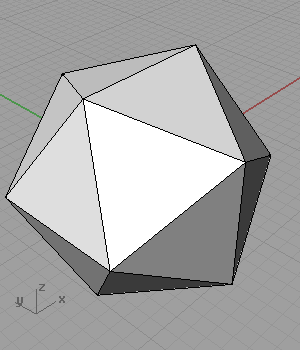
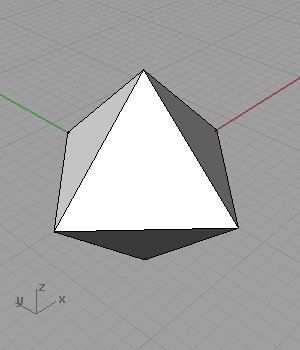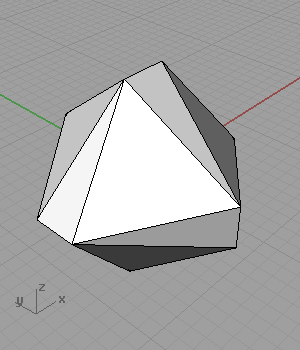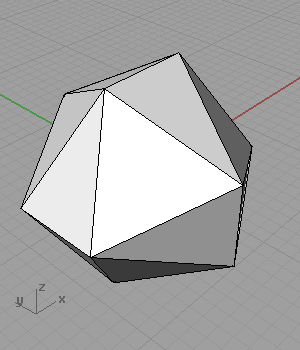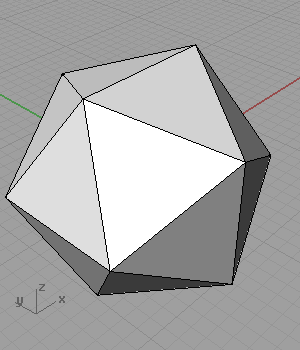
It folds, and creates octahedrons! Somehow, I stopped at this stage to think about it. Maybe I’ll try to continue to the geodesic spheres later.

Source URL: https://www.designcoding.net/icosahedron-study/

---