Hyperbolic Tessellations Continued

by Tuğrul Yazar | July 26, 2012 15:01

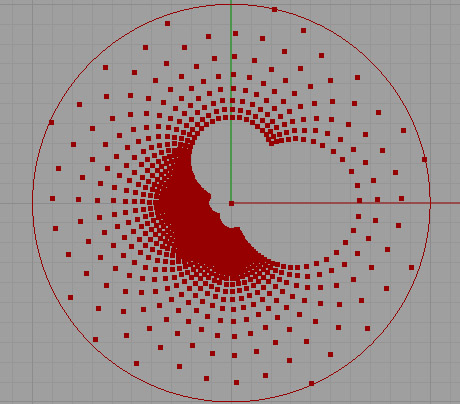
We can create tessellations of outer points in a Poincare Disk, using the manual method explained in the last post (here). But repeating that compass and straightedge process is becoming a little useless after a couple of repeats. If you say “ok. I understood the concept, let’s get faster!” then we can model just the same process in Grasshopper3D to examine varying results in seconds;

[1]

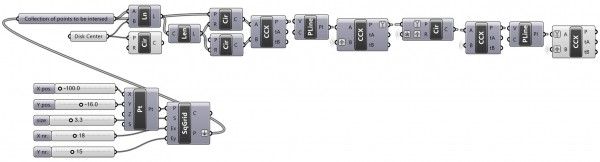
If we connect any grid of points into this definition, we can clearly see the similar result we obtained by actually projecting the hyperbolic surface onto the disk (explained here). It is fun to play with these tessellations but however, but this definition only works for points outside of the disk. I have to sit down and solve the inner points also. Here is the initial Grasshopper3D definition; [GHX: 0.8.0066][2]

Source URL: https://www.designcoding.net/hyperbolic-tesselations-continued/

---