Hyperbolic Projection of a Semi-regular Tessellation
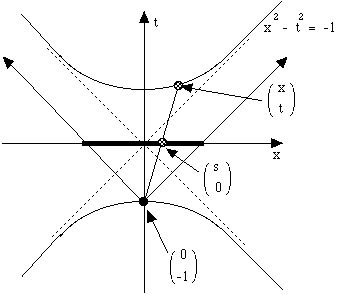
Truncated hexagonal tessellation (or named 3-12-12) is represented in hyperbolic space (as far as I understood it). The idea is simple if you don’t mix it with complex equations. Below is the 2-dimensional representation of hyperbolic projection. Paper space is defined by the thick line there. Projection is based on a two-sheet hyperboloid surface. Euclidean version of this tessellation is described here.
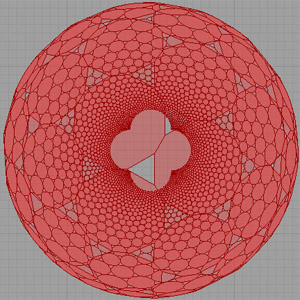
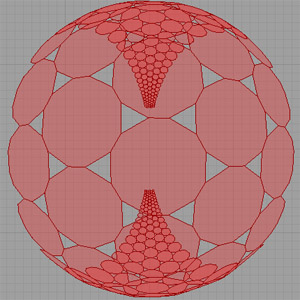
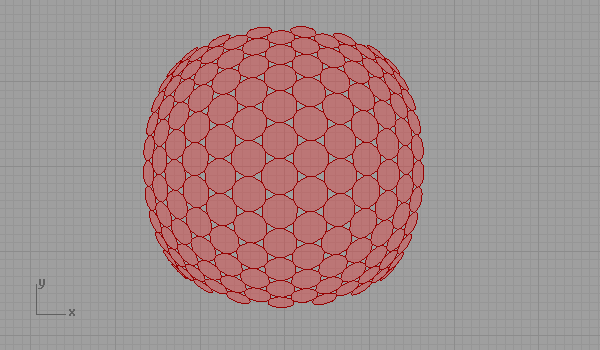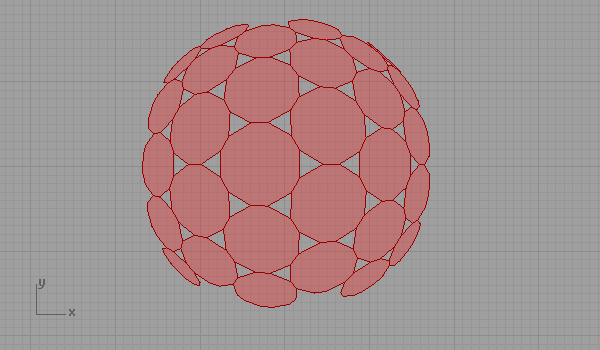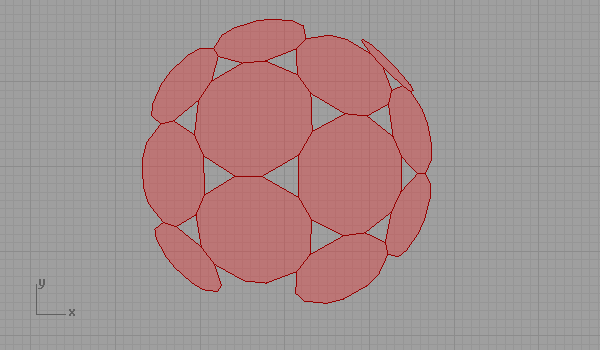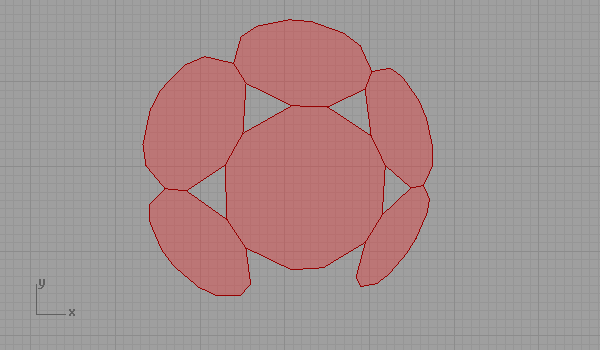
Here is the Grasshopper3D file containing the above idea of hyperbolic representation of a semi-regular tessellation. [GHX: 0.8.0066] (Don’t left-click it, right-click and save it to your computer)









