Hyperbolic Paraboloid Surface

by Tuğrul Yazar | December 30, 2011 12:17

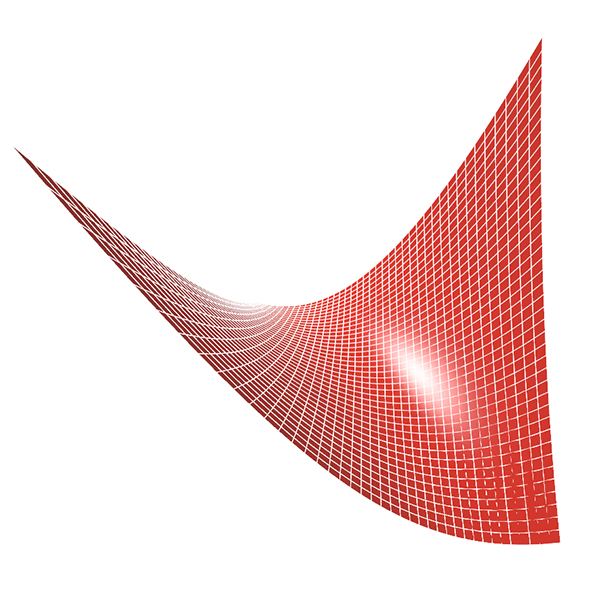
Since the mid-20th century, the hyperbolic paraboloid surface has been one of the most popular mathematical forms for architects. Named Hypar in short, this is the Quadric Surface[1] equation of the Hyperbolic Paraboloid[2]. Erik Demaine[3] summarizes several examples from architecture such as the roof of the Girls’ Grammar School in London (designed by Chamberlin, Powell, and Bonn), the Philips pavilion at the 1958 Brussels exhibition designed by Le Corbusier, and finally, Frei Otto illustrated and analyzed a grid of connecting 4-hats in the 1969 book Tensile Structures. After my initial model in 2011, it was a pleasure for me to model this old math shape again. I added a planar rotation in the parametric model so that it turns without changing the overall shape. At some point (actually at degree “pi”) it creates the other famous z=xy surface known in architecture. We should also deal with that.

This Grasshopper definition generates Hyperbolic Paraboloid surfaces with given input parameters. It is an educational and exploratory code to learn Grasshopper and generate interesting designs with it. The inputs of the definition control the surface function and the rotation parameter for animation purposes. The output of the code is a single surface in Rhinoceros. Therefore, it is ready for further investigation and modeling. The code is using native Grasshopper components. Thus, no add-ons are necessary for it to work.

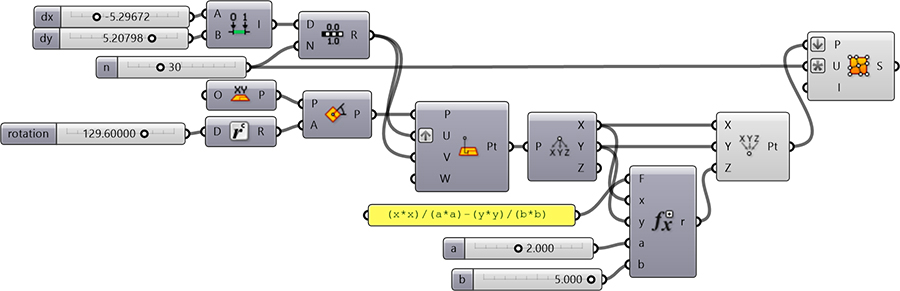
You can rebuild the definition by looking at the diagram and tutorial video. However, if you want to support my website by downloading my Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page[4] including the Grasshopper file for the Hyperbolic Paraboloid Surface and more. Thank you.

Source URL: https://www.designcoding.net/hyperbolic-paraboloid-surface/

---