Hyperbolic Space: Invert a Point
by Tuğrul Yazar | July 26, 2012 14:33
The poincare disk is still an interesting representation of hyperbolic space for me, full of mysteries. I’ve had several attempts to understand it previously (here and here). Finally, I found a resource* explaining basic concepts about it. I tried to repeat some of the constructions in Rhinoceros, (without any logical purpose). The most important part is the conversion of a Euclidean point into a hyperbolic space. There is no clear formula, for directly projecting a point into Hyperbolic space, but the method seems very interesting to me because we can do this using only a compass and straightedge. As described in previous posts, the Poincare hyperbolic space representation is an actual 3D projection that can be simulated geometrically. But from the analytic perspective, I needed proof that it can also be done with a 2D translation process.
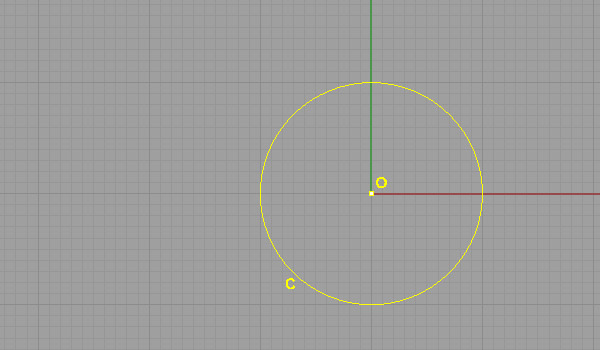
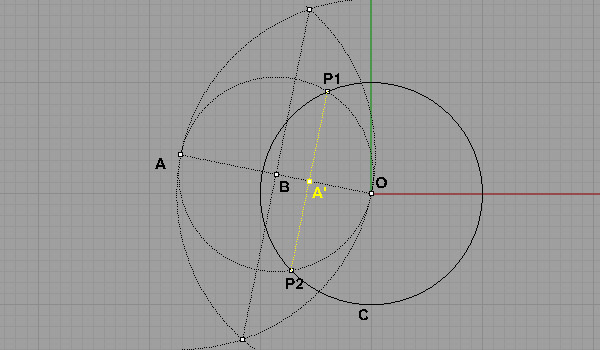
First, we draw the hypothetical Poincare Disk (a circle, named C) as we are not math people but designers, any radius is ok. Say the center is O.
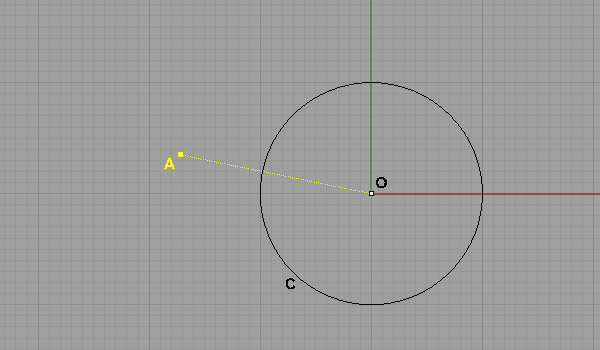
We’ll start with a point outside the disk, now, just place a point (say A) outside of it and connect O and A.
Now, we have to find the mid-point of OA. Of course with a compass and straightedge. Draw arcs from A and O with radius OA and intersect and connect those arcs to find both perpendicular direction and mid-point of OA. Call this mid-point B.
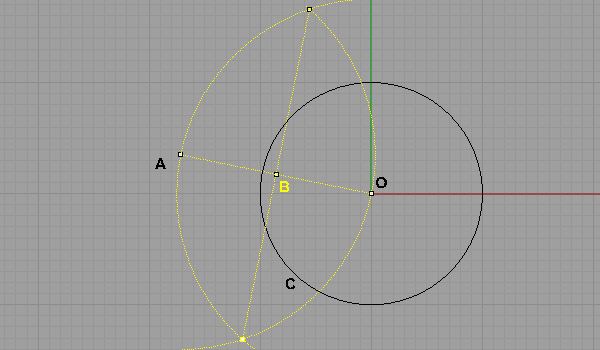
Draw a circle with center B and a radius of OB. This circle intersects disk C at two points. Call them P1 and P2.
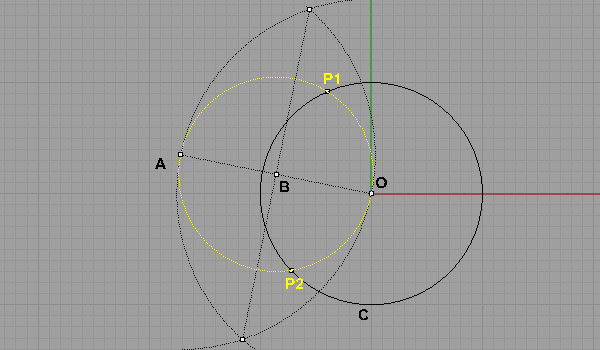
Now, connect P1 and P2 with a line and intersect it with OA. This intersection (A’) is the hyperbolic inverse of point A in the Poincare Disk.
Yes, Euclidean compass and straightedge are not powerful as contemporary CAD interfaces, but interestingly we can still benefit from them, especially in architectural geometry education. It is a way of analyzing shapes and their relations, slower but deeper. I’ll simulate this process in Grasshopper3D soon. I added a little bit more (finding mid-points for example) to the method explained here; Chaim Goodman-Strauss, (2001) “Compass and Straightedge in the Poincare Disk”, The Mathematical Association of America Monthly 108, pp.38-49
Are you bored of converting just one point? You can think of repeating the same process in Grasshopper3D and putting multiple input points to it. I’ve started that kind of definition here.
Source URL: https://www.designcoding.net/how-to-invert-a-point-in-hyperbolic-space/