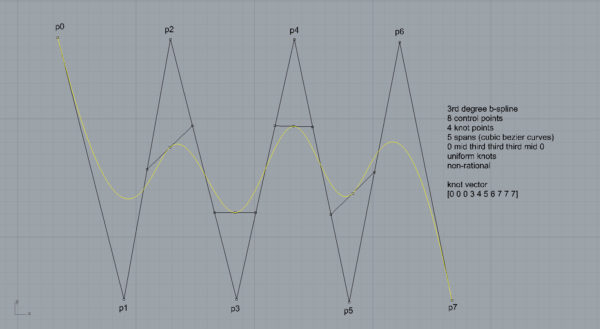
Drawing a Basis Spline with Cubic Bézier Spans

I realized this method of constructing basis splines from given control points while searching for a way to teach students about basis splines. I couldn’t find an easy and visual method to create clamped basis splines by connecting simple cubic Bézier spans. It is a tough job and requires lots of complex equations. However, I suddenly realized that there is a special way of doing that. So I decided to share this with the people searching for an easy way just like me. This method can be used to locate the knots on a basis spline, thus finding the number of Bézier spans, calculating the clamped endpoints, and finding the control points of those Bézier spans. This works with standard basis splines which are uniform and non-rational. Below is the step-by-step explanation of this method;

First, place at least 5 control points to create a basis spline of degree 3 with one knot and two Bézier spans. Connect these control points with lines:

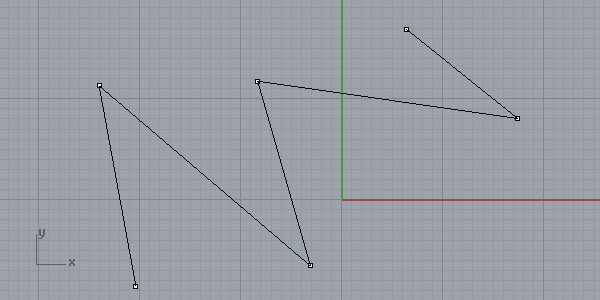
Now, skip one edge and put a point on the midpoint of the next edge, starting from both ends:

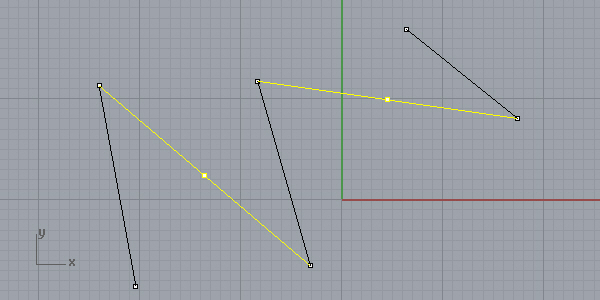
Finally, divide all remaining edges by 1/3. In my case, there is only one edge left, but it could be any number of edges:

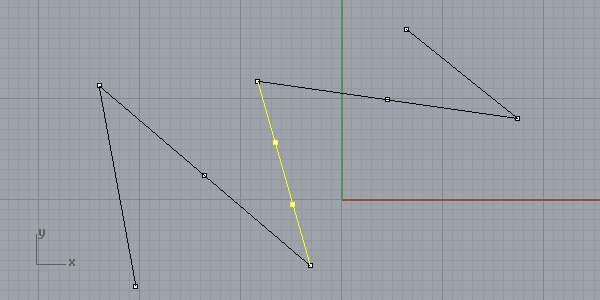
Connect those points as shown below. Midpoints of those edges will give you the “knots” of the basis spline:

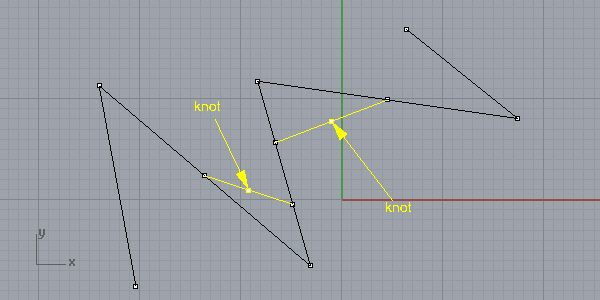
Now, the magic happens; if you draw a degree 3 NURBS span with the first points, this will be the first span of the basis spline:

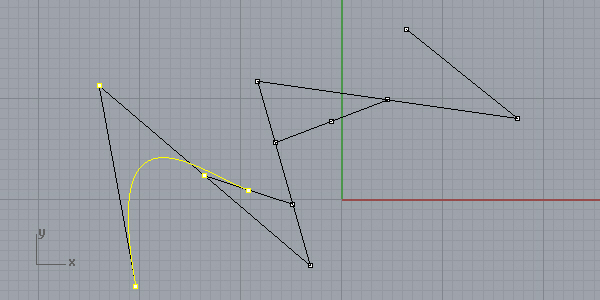
The same thing applies to other spans when you combine the points four by four. Note that we are skipping the mid-control points and choosing the division points and knots:

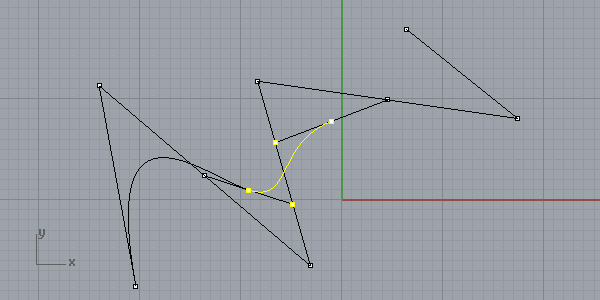
And here is the third and last span of mine. You can do this with any number of control points:

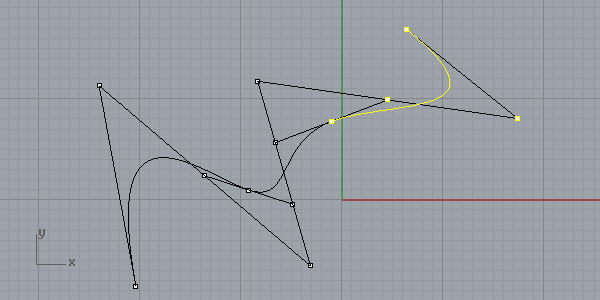
So what? Yes, it looks easy but believes me, it is not that easy to draw a basis spline with multiple control points. If you remember the Python code of the last post, I explained a method to create single Bezier curves by using simple parametric evaluations. Now, you can apply that code in any number of control points, because here, we are finding the control points of all Bezier spans. After a week-long research, I discovered this method to draw multi-control point basis splines, however, didn’t apply the Bezier span code here. Of course, this is probably not my discovery but a 500-year-old math person should have defined it. Anyway, I couldn’t find that easy explanation on the internet and had to find it myself.