Hilbert Curve

by Tuğrul Yazar | January 16, 2024 16:36

The Hilbert Curve, also referred to as the Hilbert space-filling curve, was initially introduced by the German mathematician David Hilbert in 1891. It is a continuous fractal[1] curve, presenting a variation of the space-filling Peano curves uncovered by Giuseppe Peano in 1890. After a study on the mathematical background of this curve, I implemented a Python code into Grasshopper Python. However, I wanted to explore more variations by playing with the algorithm. This is why, the resulting Grasshopper definition can generate interesting curves based on the logic of the original Hilbert Curve. Thanks to the quick and easy workflow of Grasshopper, I was able to connect the inputs and take the following animation in Rhinoceros. You can extend this study into more complex and 3d objects by further developing the Grasshopper definition.

This Grasshopper definition generates the Hilbert Curve along with some variations, based on the input parameters. You can control the number of iterations and several other parameters. It is possible to generate the original curve and explore different designs. The output of the definition is a single 2D polyline. The code is using native Grasshopper components with one Grasshopper Python code. So, you don’t need extra add-ons. This simple tool is useful if you are planning to generate space-filling fractals.

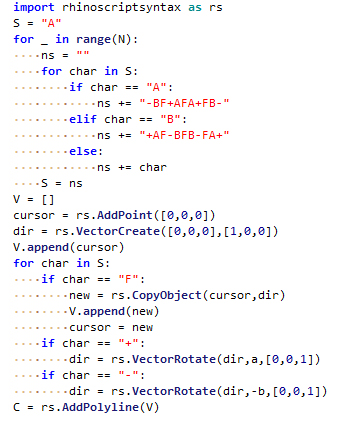
You can rebuild the definition and Python code by looking at the images above. However, would you consider being my Patreon if you want to support this website by downloading my working Grasshopper file? Here is the link[2] to my Patreon page, including the Hilbert Curve and more.

Source URL: https://www.designcoding.net/hilbert-curve/

---