The regular component design technique can be further improved by adding several manipulations. The purpose of this study was to create a surface component that reacts to an inherent parameter (actually a geodesic curve on the surface). However, within the process of parametric modeling, diverse formal potentials emerged. Most interesting results are achieved by adding a graph parameter to control the waves of reaction while splitting the surface as stripes. The definition can be downloaded here [2012_01_25-stripe]. It is created in the recently updated version (0.8.00066) of Grasshopper. This method of surface manipulation can be further improved by adding more attractors and more control over the reactions of stripes.

Unfortunately, the graph component still does not animate its values. I captured some screenshots to give you an idea of how this works in a bezier graph.

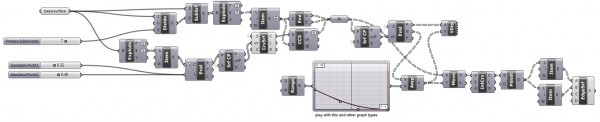
The parametric definition is simple and fast as I always prefer.

Using different graph types creates unexpected results. For example, parabola graphs reflect more dramatic bending effects on the stripes.