Goldberg Polyhedra

by Tuğrul Yazar | April 11, 2025 21:56

Although it appears[1] simple, Goldberg Polyhedra[2] in Grasshopper[3] became a tough challenge, which I like. I spent about 24 hours attempting to generate these. I started with Goldberg’s original method. This creates an equilateral triangle using coordinates denoted as m and n on a hexagonal grid. Then, we place this triangle onto the faces of an icosahedron. Finally, we project them onto a concentric sphere. We can create many polyhedra by changing the values of m and n. Up to this point, everything seemed fine. However, I could not generate planar surfaces using the Boundary Surfaces component. I tried going back and rebuilding the Goldberg Polyhedra in various ways multiple times. The Patch component worked somewhat, but still non-planar.

I learned from the literature that this is an optimization topic. Goldberg’s original method does not guarantee that all faces will be planar. So, a simpler solution came to mind. A component I’ve used in other projects, the Faceted Dome component, solved the problem quickly and elegantly. Instead of projecting the vertices of the hexagons, I now project their center points. Faceted Dome happily turns them into planar surfaces on a sphere, forming Goldberg Polyhedra. This was a bit disappointing because I wanted to derive the solution myself. However, once I realized optimization was required, it stopped being fun for me, so I decided to complete it this way. The result guarantees that each face is planar and a closed solid is formed. The Faceted Dome[4] component sometimes fails to generate the surfaces. If this happens, you can adjust the knob and make it work again.

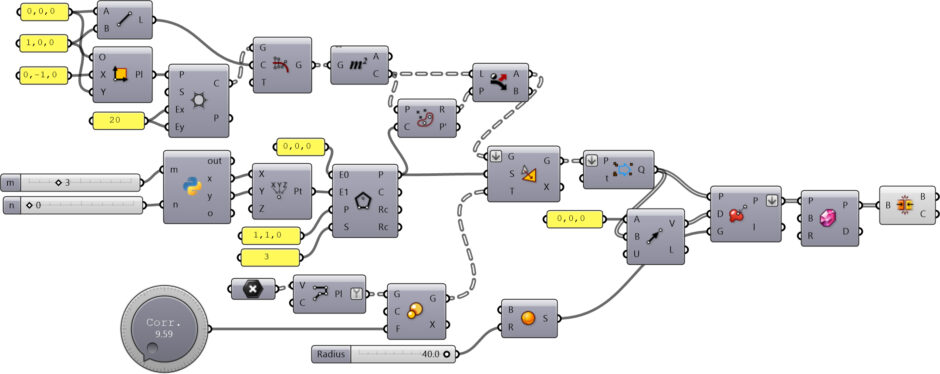[5]

You can rebuild the Goldberg Polyhedra definition using the diagram above. You’ll need the vertex coordinates of an icosahedron. You can download my working Grasshopper file from Patreon[6] to support my website. Thank you.

Source URL: https://www.designcoding.net/goldberg-polyhedra/

---