Although it appears simple, Goldberg Polyhedra in Grasshopper became a tough challenge, which I like. I spent about 24 hours attempting to generate these. I started with Goldberg’s original method. This creates an equilateral triangle using coordinates denoted as m and n on a hexagonal grid. Then, we place this triangle onto the faces of an icosahedron. Finally, we project them onto a concentric sphere. We can create many polyhedra by changing the values of m and n. Up to this point, everything seemed fine. However, I could not generate planar surfaces using the Boundary Surfaces component. I tried going back and rebuilding the Goldberg Polyhedra in various ways multiple times. The Patch component worked somewhat, but still non-planar.

I learned from the literature that this is an optimization topic. Goldberg’s original method does not guarantee that all faces will be planar. So, a simpler solution came to mind. A component I’ve used in other projects, the Faceted Dome component, solved the problem quickly and elegantly. Instead of projecting the vertices of the hexagons, I now project their center points. Faceted Dome happily turns them into planar surfaces on a sphere, forming Goldberg Polyhedra. This was a bit disappointing because I wanted to derive the solution myself. However, once I realized optimization was required, it stopped being fun for me, so I decided to complete it this way. The result guarantees that each face is planar and a closed solid is formed. The Faceted Dome component sometimes fails to generate the surfaces. If this happens, you can adjust the knob and make it work again.

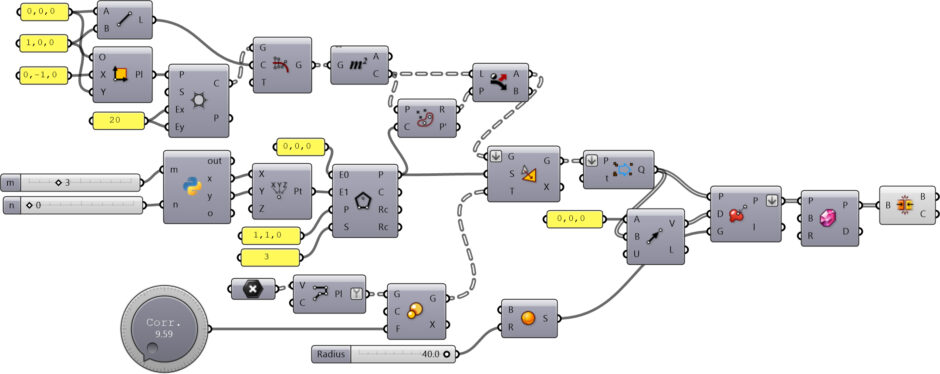
You can rebuild the Goldberg Polyhedra definition using the diagram above. You’ll need the vertex coordinates of an icosahedron. You can download my working Grasshopper file from Patreon to support my website. Thank you.