Geodesic refers to the shortest path between two points on a curved surface. It is based on the principles of geodesy, which is the science of measuring the Earth’s shape. On the other hand, in architecture and design, a geodesic dome is a spherical or hemispherical structure consisting of a network of geodesic lines (great-circle arcs) forming triangles. Therefore, the dome’s framework provides strength and stability, distributing stress throughout its structure. Buckminster Fuller popularized and developed the concept of the geodesic dome. He designed the dome based on tensegrity (tensional integrity) principles and the geodesic sphere. Fuller’s design and promotion of geodesic domes brought attention to their structural efficiency and versatility. In this short study, I developed a Grasshopper code to design thin-shell Geodesic Dome structures.

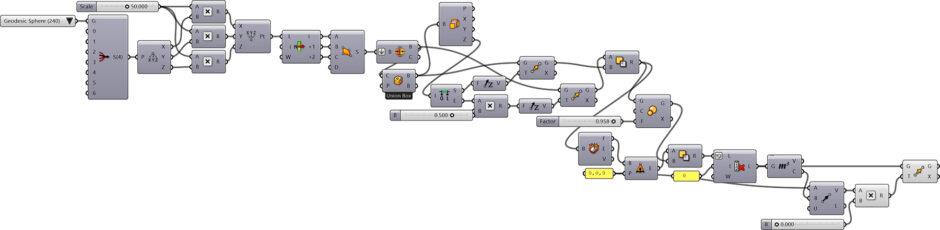
This Grasshopper definition generates variations of Geodesic Dome, including 7 types of it. The input parameters are the type of dome (number of triangles), shell thickness, displacement (you see in the animation), and the spherical ratio. A ratio of 0 creates a full dome (half sphere), and a ratio of 1 creates a full sphere. All values in between generate different dome ratios. The output of the definition is a set of closed polysurfaces for every cell of the dome. Therefore, the output is ready for 3d printing. The code is using native Grasshopper components. Therefore, no add-ons are necessary for it to work.

You can rebuild the definition by looking at the definition above. However, you will need the vertex coordinates of the Geodesic Domes. So, you can use the Parakeet add-on to get them. Thus, would you consider being my Patreon if you want to support this website by downloading my working Grasshopper file? Here is the link to my Patreon page, including the Geodesic Dome and more.