Folding Herschel’s Enneahedron

by Tuğrul Yazar | December 15, 2024 19:37

The Herschel nonahedron is a canonical polyhedron[1] whose skeleton is the Herschel graph. It has 11 vertices, 18 edges, and 9 faces. Of the edges, 6 are short and 12 are long. It is characterized by having nine faces (hence the prefix “ennea” meaning nine in Greek). In this short tutorial video, I am folding Herschel’s enneahedron. To do that, I am constructing the interior angles of this polyhedron using its unrolled net. First, I am drawing the net by using basic drawing and Euclidean construction operations. However, I skipped those parts in the video. When finished drawing the net, I folded the faces by utilizing a technique I studied earlier in the “Folding a Truncated Cuboctahedron” video.

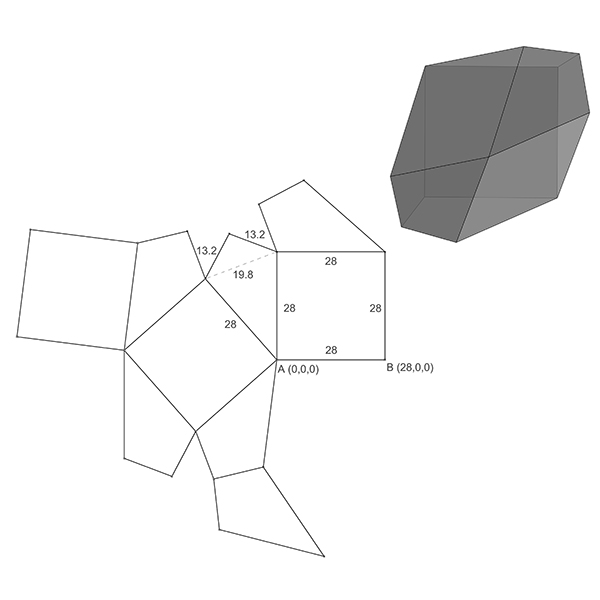
This video series showcases various in-class exercises I conducted in a freshman-year Architectural Geometry course. Using Rhinoceros[2] software, we explore Euclidean constructions, basic drawing and transformation commands, fundamental fractals, regular and semi-regular tessellations, patterns, and modeling techniques, including unrolling polyhedra. These short drawing exercises are also beneficial for junior-level architects, interior designers, industrial designers, and enthusiasts from other disciplines. I will be publishing exercises each week on my blog and other platforms. So, here is the exercise of folding Herschel’s enneahedron.

The software used in this course is Rhinoceros 3d (www.rhino3d.com[3]). However, if you want to find out more and see the whole list of this video series, you can check my YouTube channel at www.youtube.com/@designcodingnet[4] and my blog at: www.designcoding.net/[5]. You can also check my Instagram page at www.instagram.com/designcodingnet/[6]. The music of this video is ‘Ephemera’ by Scott Buckley (CC-BY 4.0). www.scottbuckley.com.au[7]

Source URL: https://www.designcoding.net/folding-herschels-enneahedron/

---