Folding a Truncated Tetrahedron
While digging through the lecture archive, I found this video I made in 2017. We introduce Platonic solids and Archimedean solids in the Design Geometry course at Istanbul Bilgi University. This video shows how we can create an Archimedean solid, the Truncated Tetrahedron, by folding it from a flat sheet. While doing this, I intersected the spheres by using the relations between the side lengths of the solid, and I calculated the rotation angles accordingly. First of all, I drew the unfolded net of the Truncated Tetrahedron. Then, I found the rotation circle of the outer vertex of one of the triangular faces. For this, I intersected two spheres from opposite vertices. Next, I repeated the same process for one of the neighboring hexagon faces. After I found its circle of rotation, I intersected these two circles. The resulting point forms the point where I will rotate the triangular and hexagonal faces and snap them. After I found this rotation angle, I rotated the other faces accordingly and closed the shape. In addition to folding a Truncated Tetrahedron, the same method can be used to fold other solids. For those who are interested in the construction of a Truncated Tetrahedron by literally truncating a tetrahedron, this post can be useful.
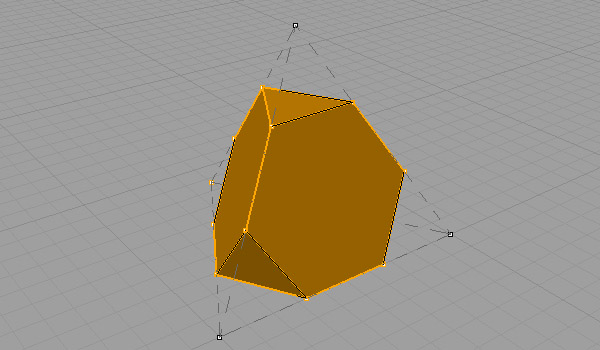
It is a good exercise both for learning the basic uses of Rhino software and for using the problem-solving steps when constructing a geometric object. But the video is a bit boring and old. Unfortunately, the image quality of the video is also not very good. I assume that in the future I can shoot videos with better quality and sound. Have to deal with it for now. Maybe in the future, somebody can re-shoot these.
Cite this post
Related Posts
Modeling and Unrolling Truncated Tetrahedron
December 14, 2024
Truncation in mathematics and geometry refers to cutting off parts of a shape, typically the vertices, edges, or other extremities, to create a new modified figure. This process is often used with polygons, polyhedra, or functions. A truncated tetrahedron is a polyhedron we can derive from a regular tetrahedron by truncating (cutting off) its four vertices. This process creates a new shape with additional faces while maintaining its symmetry. In this tutorial video, I am modeling and unrolling a truncated…
Modeling and Unrolling Truncated Tetrahedron
March 10, 2024
Truncation refers to the process of shortening something by removing parts. You can apply truncation to numbers, text, or data in various contexts. A truncated polyhedron is a geometric solid formed by truncating the vertices of a regular polyhedron. Truncation involves cutting off the corners or vertices of the polyhedron in such a way that the original faces become polygons with new edges. This process creates new faces at the truncated vertices. It often results in a shape that is…
Truncated Tetrahedron
December 21, 2011
A truncated tetrahedron is an Archimedean solid, created by slicing a tetrahedron. Its faces are regular hexagons and triangles. Assuming you’ve created a tetrahedron, first join its faces to create a closed polysurface. Now, you may recreate the lines of the tetrahedron’s edges, either by drawing them or generating them (Curve / Curve from Objects / Duplicate Edge). While the edge lines are selected, hit (Curve / Point Object / Divide Curve / Number of Segments) and type 3 to create…
Folding Truncated Cuboctahedron
December 14, 2024
A truncated cuboctahedron is an Archimedean solid, meaning it is a highly symmetrical, convex polyhedron with identical vertices and faces of regular polygons. As its name suggests, you can create the truncated cuboctahedron by truncating (cutting off) the vertices of a cuboctahedron. A cuboctahedron is a rectified cube. After you model it, you can divide all its edges into 1/3s. Then, connect those division points to draw the squares, hexagons, and octagons. In this short tutorial video, I am folding…
Modeling Truncated Icosidodecahedron
December 15, 2024
In geometry, a truncated icosidodecahedron, rhombitruncated icosidodecahedron, great rhombicosidodecahedron, omnitruncated dodecahedron, or omnitruncated icosahedron is an Archimedean solid. It is one of thirteen convex, isogonal, non-prismatic solids constructed by two or more types of regular polygon faces. In this short tutorial, I am constructing an irregular truncated icosidodecahedron. It is not the regular Archimedean solid, but a rough approximation of it. I made this model to exercise the exploration of new polyhedra by using rectification and truncation operations. Nevertheless, here…