Circle from Three Points
I learned this method from the open math resources website. I couldn’t help myself repeat it in Rhinoceros. It was quite fun to solve circle tangency problems in 2D, this is one of them: drawing the circle that passes three given points, not using ready-made commands but only geometric tools of the circle (compass) and ruler (line). Here is the sequence of it:
First of all, we need to know that the circle we are looking for is centered somewhere on the perpendicular paths between the points. This means we should find the perpendicular directions of the triangle formed by the points. Two of these perpendiculars are enough because we’ll intersect them at the end. Also, these perpendiculars should pass the midpoint between pairs. First, draw a line between any two points:
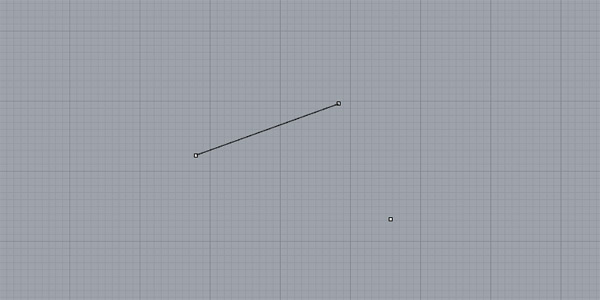
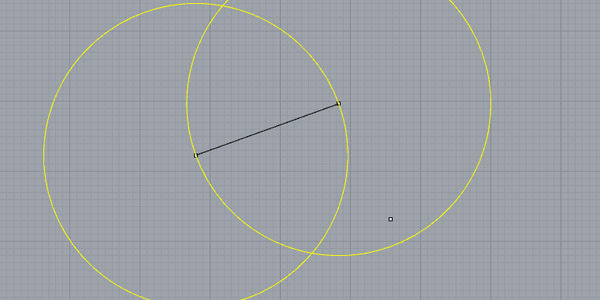
You’ll have to find the perpendicular direction (+ the midpoint) between these two points. The easiest way to do it is by drawing equal radii circles and intersecting them. The radii of these circles might be anything greater from the mid-way between these points. If they are equal circles, this will give you the midpoint of these points.
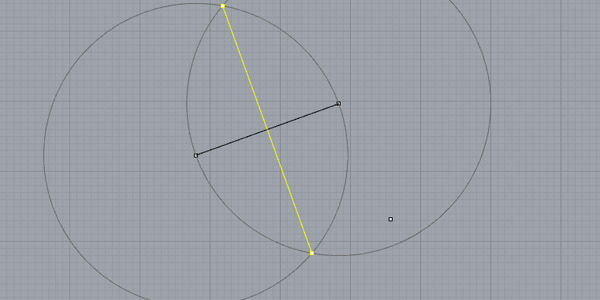
Below you see how to construct the midpoint perpendicular of any two points in space. We also use this method to find the right angle direction while drawing the square:
Now, you have to do the same for another pair of points.
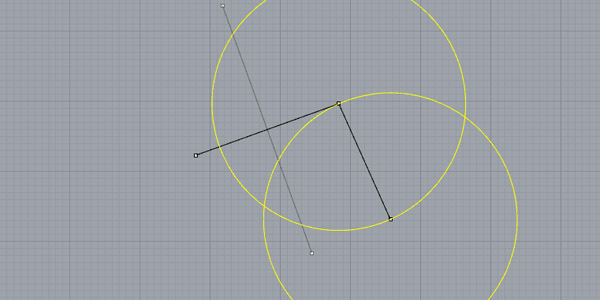
Just find the perpendicular line passing through the midpoint.
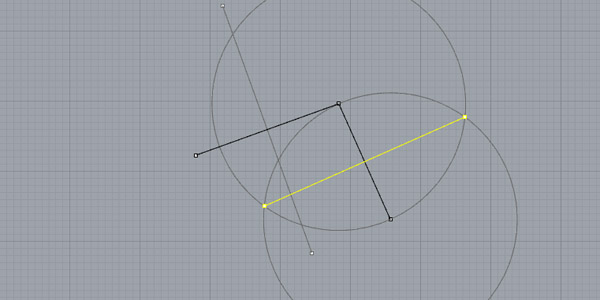
Just intersect these two perpendicular directions:
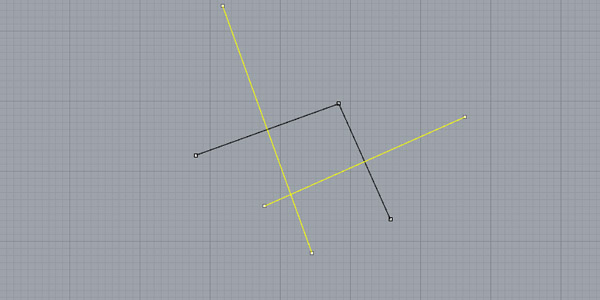
Here it is! The intersection of any two perpendicular lines will give you the center point of the circle that is equally far from every three points. It is like magic! :)
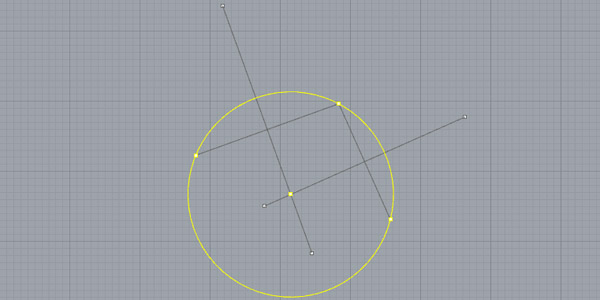
This also gives you the sphere that passes from three points (if you are not struck with Worldxy)
Cite this post
Related Posts
Constructing Tangent Circles
December 11, 2024
In geometry, “tangent” refers to a scenario where a line, curve, or surface touches another at exactly one point without crossing or leaving a gap. A tangent line to a circle is a straight line that touches the circle at only one point, and it is perpendicular to the radius at that point. Two circles can be tangent either internally or externally. Geometric constructions using a compass and straightedge can help accurately calculate tangent circles. Thus, the “constructing tangent circles”…
Tangent Circles Exercise
November 19, 2012
The first-year Architectural Geometry course includes Euclidean constructions as a study of associative geometry. We have exercised the below questions to study this topic. These are three mutually tangent circles, that can be drawn using only a compass and ruler, without built-in tangency functions in Rhino. Such exercises are expected to improve students’ reasoning. We believe architectural geometry education should encourage a conception that allows students to think about what they are doing and control their process, rather than just…
Constructing Irregular Tiling
December 11, 2024
Using a compass and straightedge enables precise geometric constructions, allowing for the creation of complex tessellations. To begin these constructions, a single starting point is sufficient. Circles, which represent a collection of points at a specific distance from the center, and straight lines, which represent a collection of points in a particular direction, are utilized for geometric constructions. In this short tutorial, we move on with the beginner-level drawing exercises. This time, I am drawing an irregular tiling with triangles…
Constructing Snub Square Tiling
December 11, 2024
Snub Square Tiling is a semi-regular tessellation of the plane, composed of two squares and three regular triangles at each vertex. The arrangement of these two regular shapes seamlessly covers the plane without any gaps or overlaps. It is one of the eight semi-regular tessellations known in geometry. The dual of Snub Square Tiling is Cairo Pentagonal Tiling, which we will explore later. In this short tutorial, I am drawing and constructing the Snub Square Tiling by using an abstract…
Drawing Koch Pentagon
December 11, 2024
The Koch pentagon is a fractal shape that starts with a regular pentagon. Here, we divide each side of the pentagon into three equal parts. Then, we replace the middle with two sides of an outward-pointing equilateral triangle. We repeat this process for every new side in each iteration, creating a self-similar pattern. Helge von Koch (1870–1924) was a Swedish mathematician known for his analysis and number theory work. He is most famous for introducing the Koch snowflake, one of…