This website explains the problem and several solutions. I managed to implement the formulas to convert a 2D square grid into spherical coordinates. The Fibonacci Sphere is one of the solutions to the equal distribution of points on a sphere. It is not the best solution to this problem. But it is regarded as a quick and efficient one. Suitable for me.

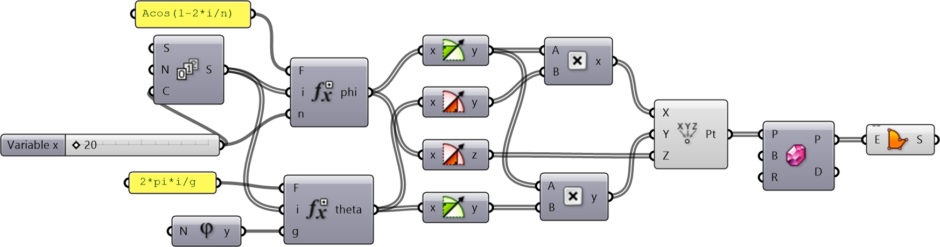
I developed this Grasshopper code by studying the above website and some other sources. The code starts with the definition of a series of numbers. The Series component gives me numbers starting from 0 to x by an increment of 1. Changing the input N affects the overall shape. For example, if you enter 0.5 to N, you will get a dome instead of a sphere. Then, two Functions are running to generate two numbers (phi and theta). In the above code, the formulas to generate these numbers are given in Panels. One of them is also using the Golden Ratio, which is a component in Grasshopper. After the generation of phi and thetas, I put them into the following formula to get the x, y, and z coordinates of points:

(x,y,z) = (cos(phi)*cos(theta), cos(phi)*sin(theta), sin(phi)

This is exactly what I am calculating at the end of the Grasshopper definition. After generating x, y, and z values, I place points. Finally, I added a Faceted Dome component to visualize the surfaces. Changing the number of points on the sphere creates the below animations:

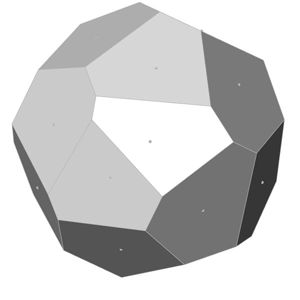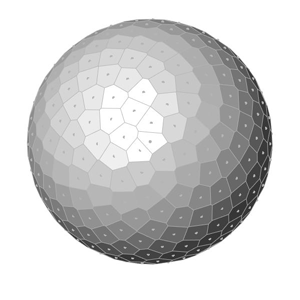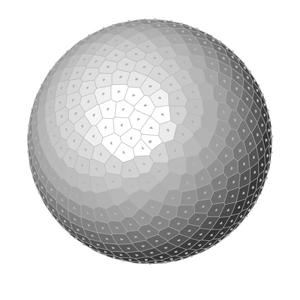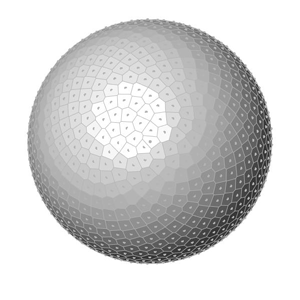
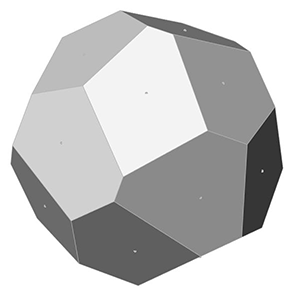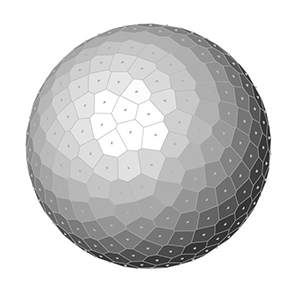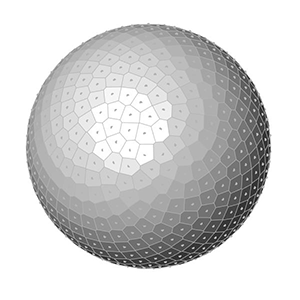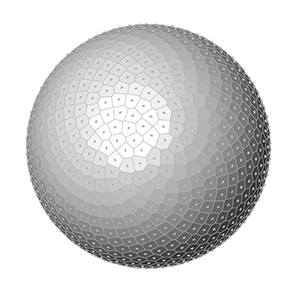
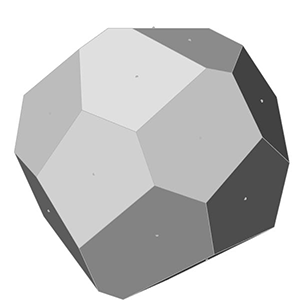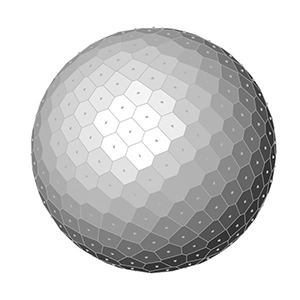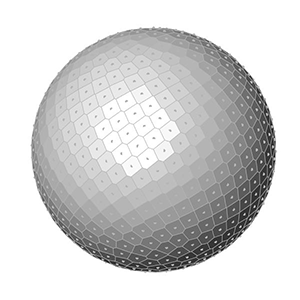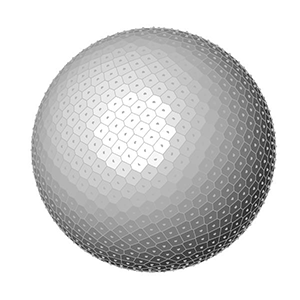
You can re-build the definition by looking at the image above and the explanation. However, if you liked this content and want to download the Grasshopper file; would you consider being my Patreon? Here is the link to my Patreon page including the working Grasshopper file for the Fibonacci Sphere.