Fibonacci Dome
by Tuğrul Yazar | March 1, 2024 22:34
This is the continuation of my previous study on the Fibonacci lattice on a spherical surface, creating a Fibonacci Dome structure. The panelization of curved forms with flat surfaces has been a favorite topic in architectural geometry. The trigonometric layout of the Fibonacci sequence generates a spherical formation, while the Faceted Dome component handles planarity. Here I further enhanced the previous code into a pavilion design. The essential part of the code is about the placement of points on the half sphere by checking the Z coordinate of the calculated points. Finally, I extruded the faces for the thickness of the panels. There are many variation possibilities in this dome design.
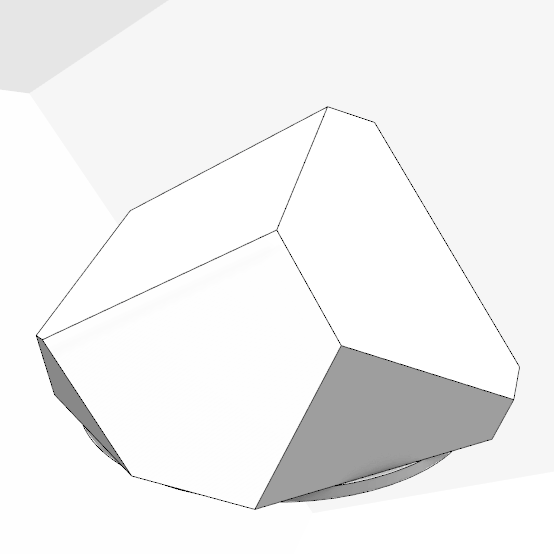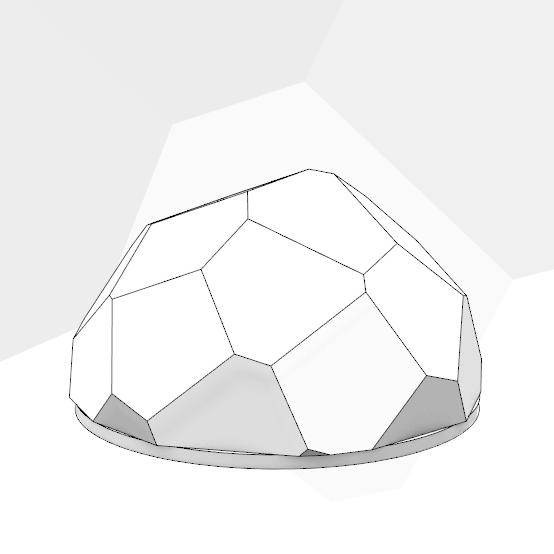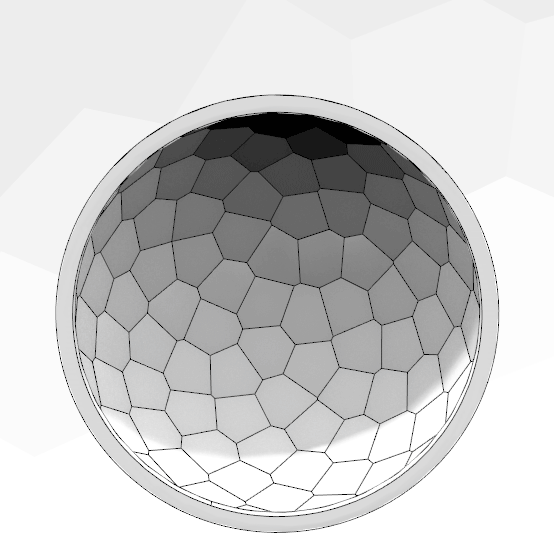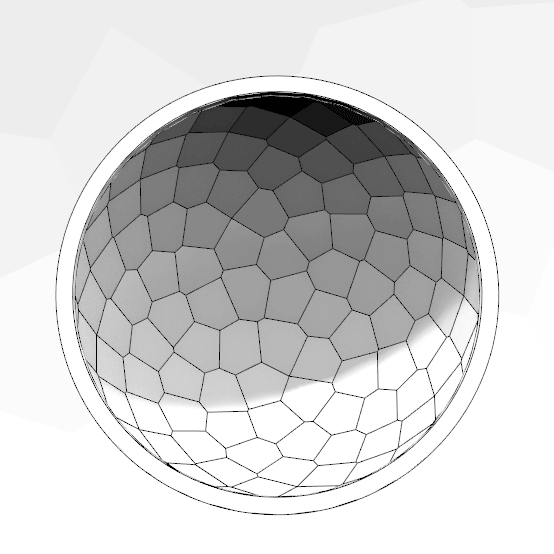
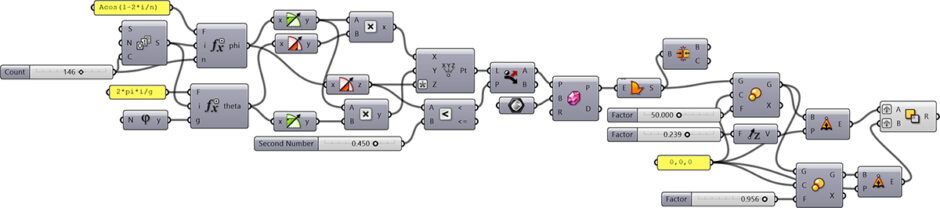
This Grasshopper definition generates the variations of Fibonacci Dome structures with several input parameters. The user-controlled inputs are the n variable which controls the number of Fibonacci points, the radius/height ratio of the dome, and the thickness of the dome pieces. The resulting objects are closed polysurfaces. Therefore, it creates the essential data for the production of a potential structure on any scale. I made the definition with the help of the native Grasshopper components in Rhinoceros 7. So, you don’t need to install any add-on to be able to use it.
 [1]
[1]You can rebuild the definition by looking at the diagram above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? The link to my Patreon page[2] includes the working Grasshopper file for the Fibonacci Dome and more. Thank you.

- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2024/03/Fibonacci-Dome-def.jpg
- The link to my Patreon page: https://www.patreon.com/posts/fibonacci-dome-99547249?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
Source URL: https://www.designcoding.net/fibonacci-dome/