Fibonacci’s Spiral with Rhino Python

by Tuğrul Yazar | July 30, 2017 16:12

Studied earlier in Grasshopper here[1], the sunflower spiral or Phyllotaxis, or Fibonacci’s spiral could be drawn as an exercise of looping in Rhino Python[2].

import rhinoscriptsyntax as rs
import math
s = 137.508
for n in range(0,500):
    t = math.sqrt(n)
    g = n * s
    z = rs.Polar([0,0,0],g,t)
    rs.AddCircle(z,0.3)

According to ChatGPT[3]:

Phyllotaxis is the arrangement or patterning of leaves, flowers, or other plant parts around a stem or axis. Thus, it refers to the specific geometric arrangement of these structures in plants. The term “phyllotaxis” comes from the Greek words “phyllon” (meaning “leaf”) and “taxis” (meaning “arrangement” or “order”).

Phyllotaxis can vary widely among different plant species, and it often follows specific mathematical patterns. One of the most well-known patterns is the Fibonacci sequence, in which each number is the sum of the two preceding ones (e.g., 0, 1, 1, 2, 3, 5, 8, 13, …). In some plants, the number of spirals or whorls of leaves or other plant parts follows the Fibonacci sequence. This results in a visually appealing arrangement.

If you are new to Rhino Python, you may wonder how you are going to write this code. Just type EditPythonScript in the Rhino command bar and open the Python editor. Then, write the code you see above and hit F5 to run it. So, you will see Fermat’s spiral drawn with circles in the Rhino viewport. Alternatively, I prepared a Grasshopper definition including the same Python code as a component. Here it is:

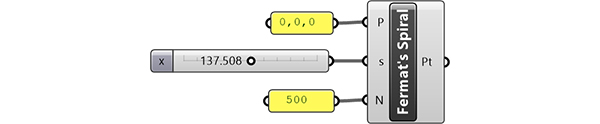
You can rebuild this by typing the code above in the Rhino Python editor. However, if you want to support this website by downloading my Grasshopper file including the Python component; would you consider being my Patreon? Here is the link to my Patreon page[4] including the working Grasshopper file for the Fibonacci’s Spiral and more. 

Source URL: https://www.designcoding.net/fermats-spiral-with-rhino-python/