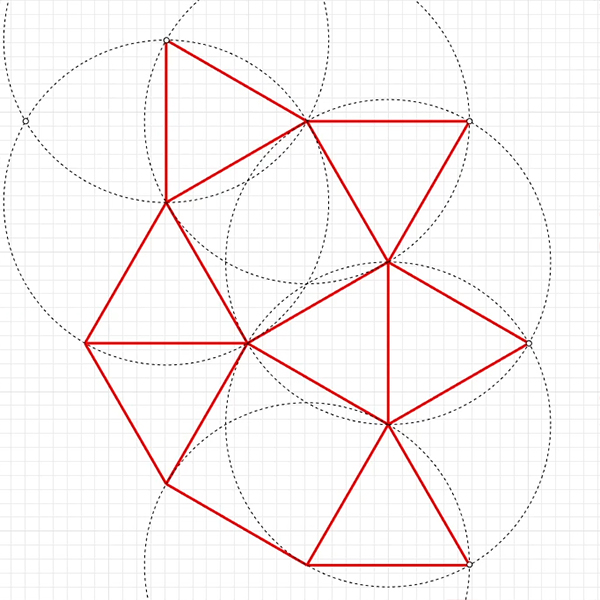
Euclidean Construction of Snub Square Tiling
The snub square tiling is one of the semi-regular tessellations, where regular triangles and squares match perfectly to fill the plane without gaps or overlaps. The Euclidean construction of Snub Square tiling is possible by utilizing the basic compass and straightedge operations. I made this construction in Rhinoceros to show that there is no need for any numerical input to locate the points and draw the tiling. There are two major techniques explained there. One of them is the basic method to draw triangles by using a compass or a circle. The other is the calculation of the right angle (90 degrees) without any number but only geometric construction. This ancient art and science is still interesting and educational for the basics of architectural geometry.
The snub square tiling is also named 3.3.4.3.4 since at any vertex, these are the polygons around it. The name comes from the snub operation which includes expanding and twisting. This tiling is the result of the snub operation on a regular square tiling.
I studied the Euclidean construction of snub square tiling many times before. After those years, trying and executing this construction sequence is still funny and motivating. I generated this tiling in Grasshopper here. However, drawing in Rhino or any other CAD software seems to be easier than coding this. The drawing usually starts with a random line on the plane. The process includes the drawing of two regular triangles. Then, I proceed by finding the right angle direction, normal to any segment of these triangles. This requires two identical intersecting circles that are on the same axis as the segment. The radius of these circles doesn’t matter as long as they intersect. Also, this requires the distance transferring via the copy command in Rhino.
Cite this post
Related Posts
Constructing Snub Square Tiling
December 11, 2024
Snub Square Tiling is a semi-regular tessellation of the plane, composed of two squares and three regular triangles at each vertex. The arrangement of these two regular shapes seamlessly covers the plane without any gaps or overlaps. It is one of the eight semi-regular tessellations known in geometry. The dual of Snub Square Tiling is Cairo Pentagonal Tiling, which we will explore later. In this short tutorial, I am drawing and constructing the Snub Square Tiling by using an abstract…
Constructing Irregular Tiling
December 11, 2024
Using a compass and straightedge enables precise geometric constructions, allowing for the creation of complex tessellations. To begin these constructions, a single starting point is sufficient. Circles, which represent a collection of points at a specific distance from the center, and straight lines, which represent a collection of points in a particular direction, are utilized for geometric constructions. In this short tutorial, we move on with the beginner-level drawing exercises. This time, I am drawing an irregular tiling with triangles…
Euclidean Construction of Rhombitrihexagonal Tiling
March 1, 2024
The rhombitrihexagonal tiling is one of the semi-regular tessellations. It is composed of regular hexagons, squares, and triangles. It is a periodic tessellation since you can copy the fundamental unit and move it across the plane to generate the tiling. I use this quality of the tiling to draw and expand it in Rhinoceros software. This is a basic drawing exercise. At the same time, it is a nice exercise for the mind and sometimes for the soul. There are…
Snub Square Surface
February 20, 2013
For the last 10 days, I’ve been searching for a proper algorithm for representing surfaces using planar shapes. It is obvious that triangulation is an answer but there is an interesting research topic of planar remeshing using shapes other than quads, hexagons, or any other regular polygons. Especially in computer graphics, such things refer to the optimization of models to decrease the load of GPUs. In the Grasshopper community, this has also been discussed and there is a great implementation…
Snub Square Tiling
October 22, 2012
Here is the step-by-step generation of the old Snub Square Tiling. Frankly, this is the first step in the generation of Cairo Pentagonal Tiling I generated with Grasshopper earlier. Because Cairo pentagonal is the dual of a snub square. The first step was easy. Just dispatch cells of a square grid, then evaluate them according to the ratio of 0.366 approx. which is derived from the bisector of an equilateral triangle. Now, we have a snub square tiling, composed of…