Euclidean Construction of Rhombitrihexagonal Tiling

by Tuğrul Yazar | March 1, 2024 14:01

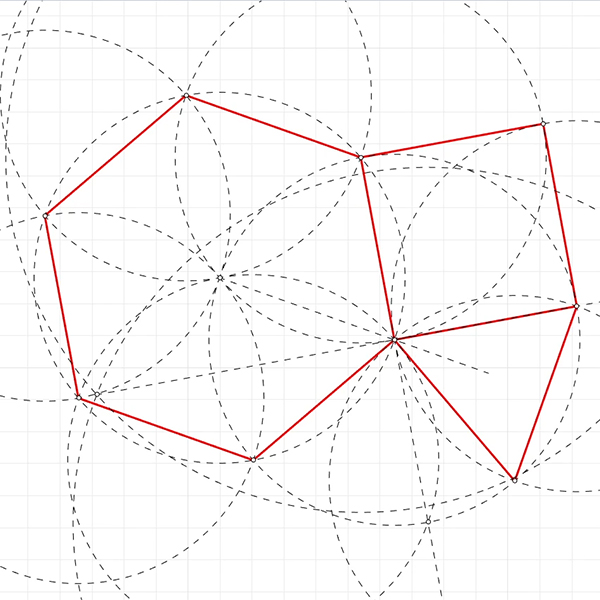
The rhombitrihexagonal[1] tiling is one of the semi-regular tessellations. It is composed of regular hexagons, squares, and triangles. It is a periodic tessellation since you can copy the fundamental unit and move it across the plane to generate the tiling. I use this quality of the tiling to draw and expand it in Rhinoceros software. This is a basic drawing exercise. At the same time, it is a nice exercise for the mind and sometimes for the soul. There are only 8 such tilings that fill a 2D plane without gaps or overlaps. I made the Euclidean construction of rhombitrihexagonal tiling with an abstract compass and straightedge. So, the step-by-step process is fully deterministic and precise, though not requiring any numerical input.

The rhombitrihexagonal tiling is also named 3.4.6.4 since at any vertex, these are the polygons around it. It is one of the regular lattices for circle packings.

This was the first time I drew this tiling with the Euclidean construction method. It is quite possible to generate this tiling in Grasshopper or any other programming language. However, drawing in Rhino or any other CAD software seems to be an educational and relaxing experience. I start the Euclidean construction[2] of rhombitrihexagonal with a random line on the plane. The process includes the drawing of the regular hexagon with a series of compass operations.  Then, I proceed by finding the right angle direction, normal to any segment of this hexagon. This requires two identical intersecting circles that are on the same axis as the segment. The radius of these circles doesn’t matter as long as they intersect. Also, this requires the distance transferring via the copy command in Rhino.

Source URL: https://www.designcoding.net/euclidean-construction-of-rhombitrihexagonal-tiling/

---