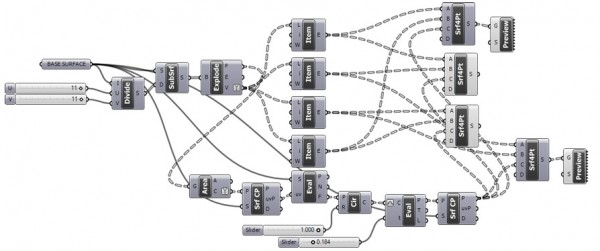
After Puzzling, I tried to establish more of Escher’s basic grid transformations using Grasshopper’s native components. This definition simulates Escher’s transformation of four-cornered grids. The postulate is based on the fact that every quadrilateral (or triangular) planar shape can create regular tessellations without gaps or overlaps. In the traditional method, this tessellation is achieved by rotating the shape 180 degrees and copying afterward. However, in Grasshopper we simply define the fifth point for each shape and divide subsurfaces into four triangular surfaces.

There are also more complicated methods of Escher that should be considered in the education of architectural geometry. Here is the Grasshopper definition [GH: 0.8.0066] and [3DM: Rhino 4].