Dürer Rhombii
by Tuğrul Yazar | November 19, 2013 10:36
I’ve come across this nice website[1] about the short history of tilings and tessellations. In this post, I am regenerating a tiling of Dürer rhombii. Albrecht Dürer[2] sounds like one of the pioneers of some of the concepts of today’s emerging field of architectural geometry. Here is a phrase from that website about Dürer;
“…Like Kepler, regular polygons and polyhedra fascinated Dürer… A large section of the Painter’s Manual is dedicated to practical ways to construct various curves and regular polygons with a ruler and compass. Kepler goes over some of the same ground in the first book of Harmonices Mundi but only includes mathematically exact constructions. The more pragmatic Dürer also includes approximations, including one for the regular heptagon[3]. (One can prove that there is no exact construction using a ruler and compass for this shape.)…”
“…Dürer was one of the first people to provide flat paper models folded into polyhedra. He provides more than a dozen examples… The Painter’s Manual also includes a brief section on polygon tilings. Dürer illustrates the three regular tilings consisting respectively of squares, triangles, and hexagons, as well as the 4.8.8 octagon tiling and the 3.6.3.6 uniform tiling with its striking six-pointed star pattern. He also shows examples of non-edge-to-edge tilings with triangles and squares..”
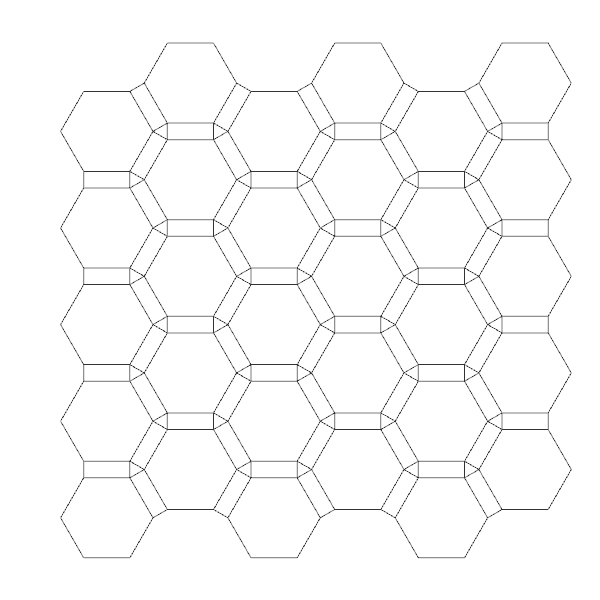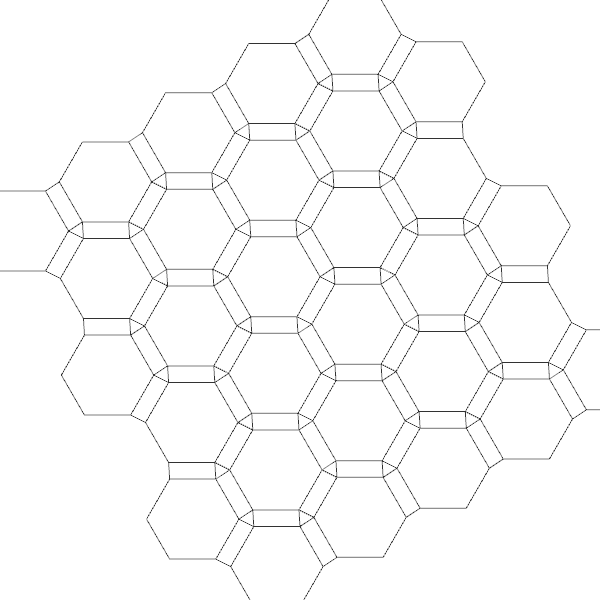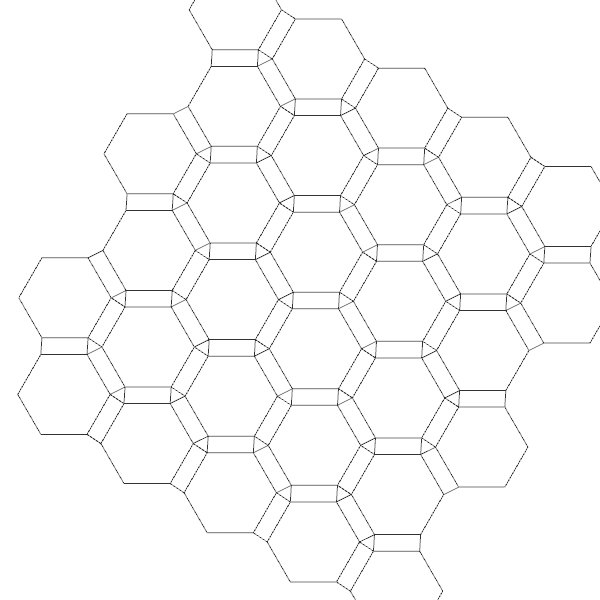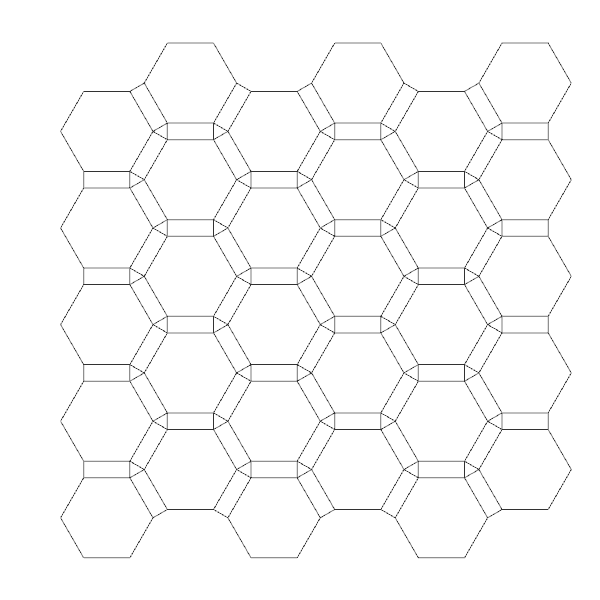
Here I developed Grasshopper code for one of the rhombic tilings from that website. I like these tilings. Because they open new variations to the seemingly limited area of tessellations;
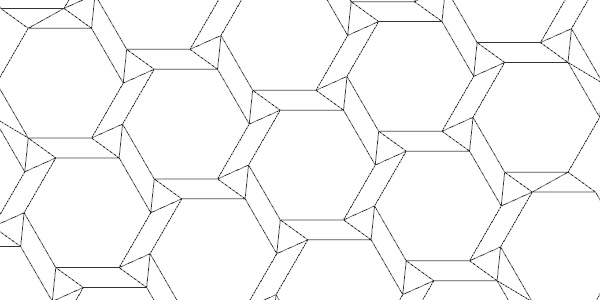
 [4]
[4]Here is the Grasshopper definition file for Dürer Rhombii:
- this nice website: http://gruze.org/tilings/
- Albrecht Dürer: https://tr.wikipedia.org/wiki/Albrecht_D%C3%BCrer
- regular heptagon: http://demonstrations.wolfram.com/AlbrechtDurersHeptagonOf1525/
- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2013/11/2013_11_18-hexsemi-def.jpg
- Download: https://www.designcoding.net/decoder/wp-content/uploads/2013/11/2013_11_18-hexsemi.ghx
Source URL: https://www.designcoding.net/durer-rhombii/