Drawing Gosper Curve

by Tuğrul Yazar | December 10, 2024 23:45

The Flowsnake, or Gosper curve is a space-filling[1] fractal[2]. It is also known as the Peano-Gosper curve. There are other similar space-filling fractals such as the Dragon curve, or the Hilbert curve. A space-filling fractal is a special type of curve, that fills a plane when iterated infinitely. This means, that if you continue to replace every segment of the polyline with the whole drawing, it will quickly become very dense and ultimately fill the plane without any gaps or overlaps. Drawing the Gosper curve is the continuation of the previous exercise[3] of drawing the Gosper unit. Here, we generate the fractal using the basic drawing and transformation functions of Rhinoceros[4].

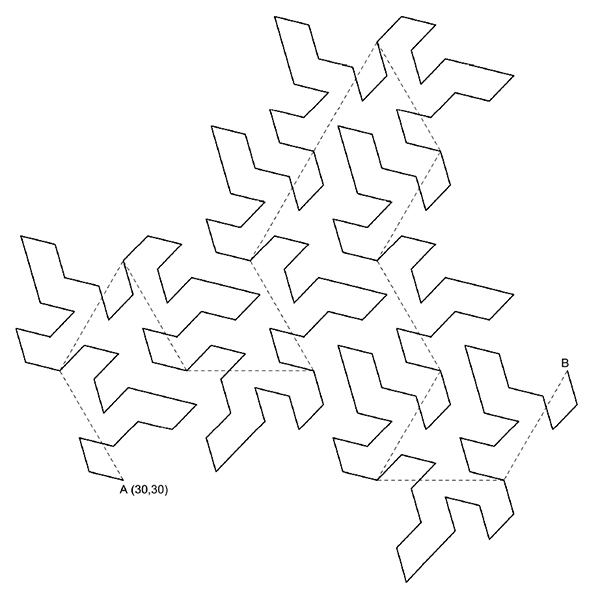
I have been conducting a series of in-class exercises in the freshmen year Architectural Geometry course, focusing on Euclidean constructions, basic drawing and transformation commands, introductory fractals, regular and semi-regular tessellations, patterns, modeling, and unrolling polyhedra using Rhinoceros software. Junior architects, interior designers, industrial designers, and enthusiasts from other disciplines can benefit from these concise drawing exercises. I will try to publish exercises every week on my blog and other platforms. So, this week’s exercise is; drawing the Gosper curve:

The software used in this course is Rhinoceros 3d (www.rhino3d.com[5]). However, if you want to find out more and see the whole list of this video series, you can check my YouTube channel at www.youtube.com/@designcodingnet[6] and my blog at: www.designcoding.net/[7]. You can also check my Instagram page at www.instagram.com/designcodingnet/[8]. The music of this video is ‘At The End Of All Things’ by Scott Buckley (CC-BY 4.0). www.scottbuckley.com.au[9]

Source URL: https://www.designcoding.net/drawing-gosper-curve/

---