Dragon Curve Fractal

by Tuğrul Yazar | December 25, 2023 17:56

This week’s fractal[1] is the famous Dragon Curve. Dragon Curve exhibits self-similarity[2], meaning parts of the curve resemble the overall shape, regardless of scale. It’s fascinating because a relatively simple construction process generates a complex and visually captivating fractal pattern. The Dragon Curve is often used to demonstrate fractal properties in mathematics and is popular in recreational mathematics due to its intricate and beautiful patterns. It has applications in computer graphics and is interesting in studying chaos theory, self-similarity, and the nature of fractals. Apart from its technical beauty, It is possible to use it in a purely decorative way. This is why, I added a design feature to make it more exploratory. I may add a thickness feature in the future to make it producible with digital fabrication.

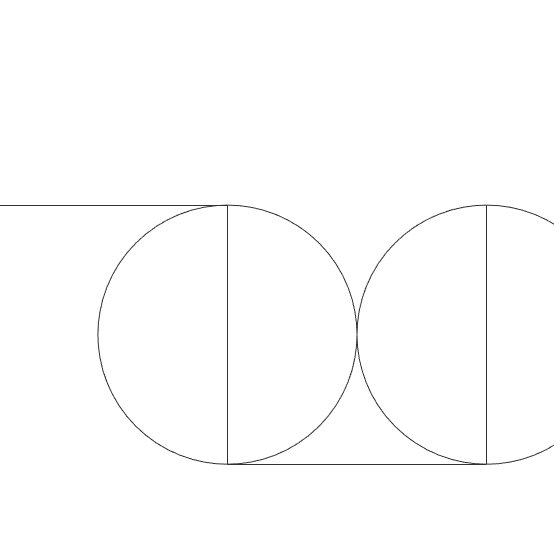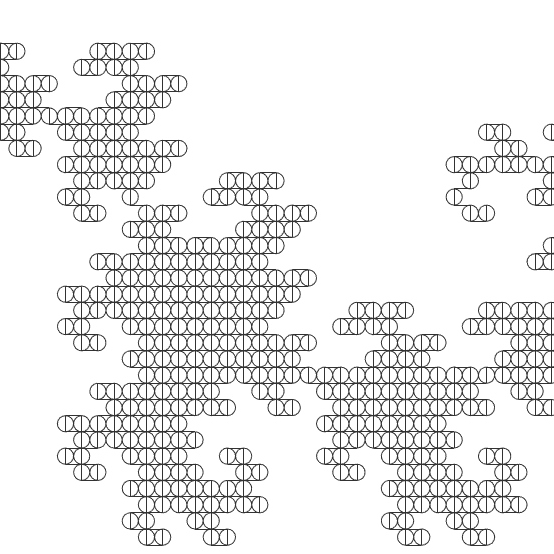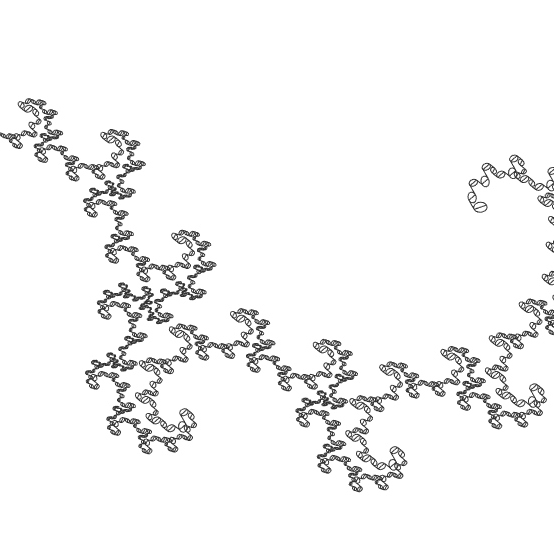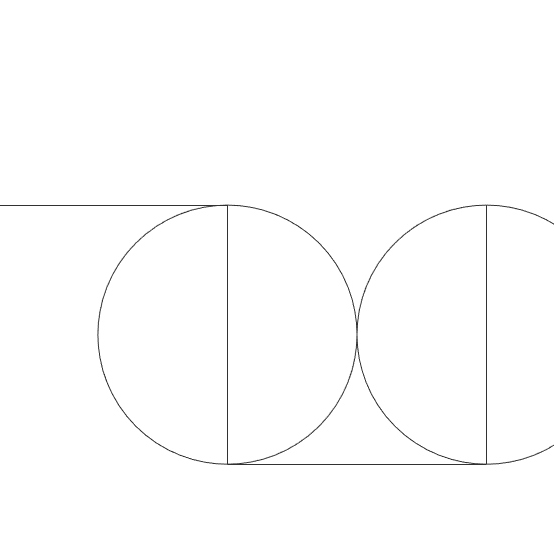
This Grasshopper definition generates Dragon Curve Fractal with several input parameters. The initial generator shape, and of course, the number of iterations to process. It is possible to re-generate the classical Dragon Curve and explore new designs (with the help of the TriMap component). The result includes piecewise polylines. Therefore, it is ready for printing on any scale. I made the definition with the help of the Anemone components in Rhinoceros 7. So, you need to install it from food4rhino[3] first, to be able to use the definition.

You can rebuild the definition by looking at the diagram above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? The link to my Patreon page[5] includes the working Grasshopper file for the Dragon Curve Fractal and more. Thank you.

Source URL: https://www.designcoding.net/dragon-curve-fractal/

---