Delaunay Triangulation on Surface

This is a useful tip both to solve some of the problems with custom surface subdivisions, and to explain the uses of parametric surface evaluations (the U, V, W thing) and the practical use of data lists.

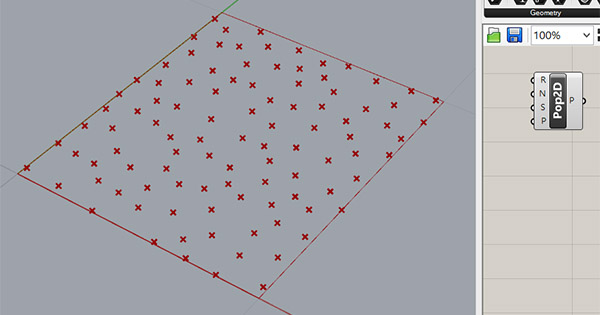
Step 1: Put your points inside 0,0,0 and 1,1,0 so that the resulting coordinates can easily be converted to U and Vs. In the example, we are putting some random points between 0,0 and 1,1 using the Populate2d component.

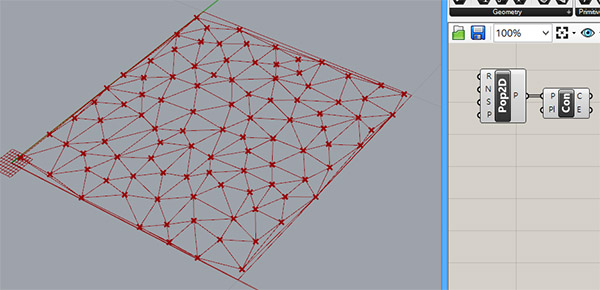
Step 2: Then make whatever you want with these points. For example, we can create a Voronoi subdivision or Delaunay triangulation, or just draw something with a polyline there. This will be the drawing that is to be mapped onto the surface.

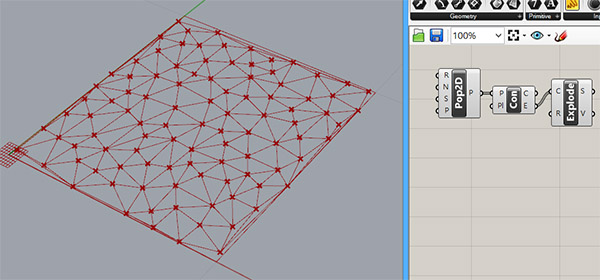
Step 3: Explode the curves generated in Step 2 so that we’ll have the vertex connectivity sequences as a data list (or tree).

Step 4: Just evaluate the surface using the vertex coordinates as U, and V values. Now the points should be on the surface if you choose “reparameterize” for the S input.

Step 5: Finally join these mapped points again as a polyline to see that the explode operation did a good job in maintaining the order of the vertices so that we could easily re-create the curves on the surface.