Delaunay Exercise

by Tuğrul Yazar | June 28, 2013 23:53

After becoming a ready-made component in Grasshopper, the Delaunay triangulation lost its popularity quickly. It used to be a nice problem of computational geometry for designers obsessed with scripting.  Last month, Benay reminded me of the method of circle checking. She showed her Rhinoscript that creates circles from point triplets and checks if a point is inside or not. Today I studied this in Grasshopper to see if I can handle the required point combinations quickly. However, my first attempt was terrible.

Wikipedia has a clean-quick explanation of the term:

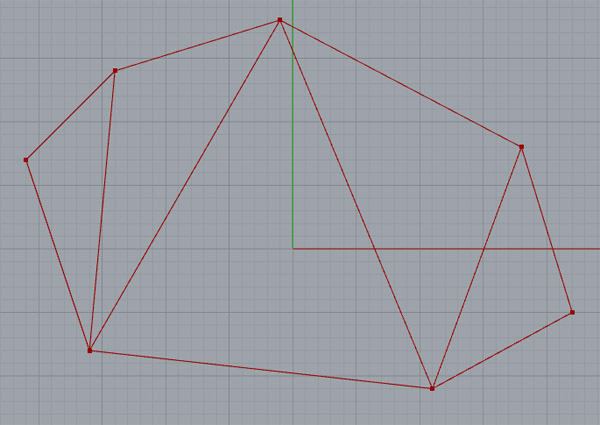
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid skinny triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.

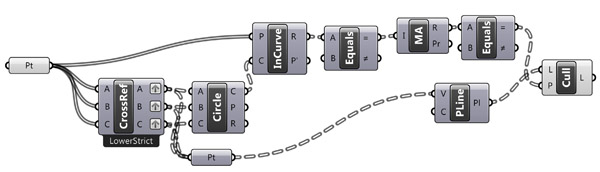
After a couple of dead ends, I solved it. Here is the Grasshopper definition: [GHX: 0.9.0056][1]. The best part was understanding the “cross reference” component. It is a brute-force approach, creating all possible triangles from a given list of points. By using the combination formula I calculated the correct number of triangles. However, the different modes of the “cross reference” component give different results. “Lower strict” mode was the one I want, which calculates every combination of point triplets without caring about their order. I studied it with other native Grasshopper components but it became too complicated. After finding all of the circles. I checked if any point is inside these circles. If there is no point inside the circle, then these three points create a cell of the Delaunay triangulation. I checked with the ready-made component and it works correctly. But in some conditions, the circle component gives an error as three linear points cannot create a circle.

Source URL: https://www.designcoding.net/delaunay-exercise/

---