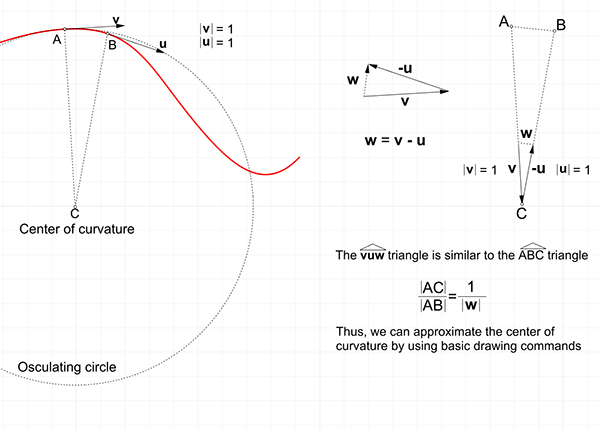
Curvature can be roughly described as how much a curve is “turning” at point a P. We place two “very” close tangents and measure the difference between them. The closer these tangents are, the more precise our approximation would be. An osculating circle is a tangent circle that has the same curvature as the curve at point P. The larger the circle, the more “flat” the curve is. An infinitely large osculating circle means the curve is linear at point P. Another term, the center of curvature represents the center point of the osculating circle. Rhino can calculate these with the Curvature command quickly and easily. However, I wondered how I could calculate them manually. In this tutorial, I am attempting to make a curvature approximation by drawing commands in Rhinoceros. These are line, circle, point, and scale.

I am using the similar triangles approach and trying to locate the center of curvature by using two tangents with equal Euclidean distance on both sides of a point. So, I did this easily by drawing a circle. The smaller this circle is, the better our approximation would be. Then, I created a triangle and scaled it so that it would become the same size as the triangle formed by the center of curvature.

While drawing and testing, I realized that I could also do this by only using Euclidean compass and straightedge, since I can draw and extend the normal directions with them. So, instead of using the scale command, I can do the same calculation by drawing two normal directions and extending them until they intersect. However, this is another story. You can find the curvature approximation by drawing and more on my other social media. Thank you for watching.