Contour-fold Structure
by Tuğrul Yazar | February 1, 2015 17:03
Euclidean constructions, when represented computationally, rely on algorithms and mathematical principles to generate geometric shapes and forms. Through precise calculations and logical operations, a computer program can emulate the actions of a compass and straightedge, constructing lines, circles, and polygons with accuracy and efficiency. These digital incarnations of Euclid’s timeless techniques enable the exploration of geometric concepts and the creation of visually captivating representations. This project is interesting because of the Euclidean construction underneath. Initially, I studied this type of structure nine years ago, here[1] and here[2]. I call this new version the Contour-Fold structure. The original inspiration is the Rising Chair by Robert van Embricqs[3]. The user of my simple tool can define and modify the path curves of the hinges and apply the folding simulation with a number slider. It was a nice and calming exercise of the Euclidean compass-ruler method to simulate this folding motion in Grasshopper.

This Grasshopper definition generates contour-fold structures with several input parameters. The folding paths, number, width, and length of the stripes are the user-controlled inputs. The resulting objects are closed polysurfaces and polylines. Therefore, it creates all the necessary data for the production of a potential structure on any scale. I made the definition with the help of the native Grasshopper components in Rhinoceros 7. So, you don’t need to install any add-on to be able to use the definition.
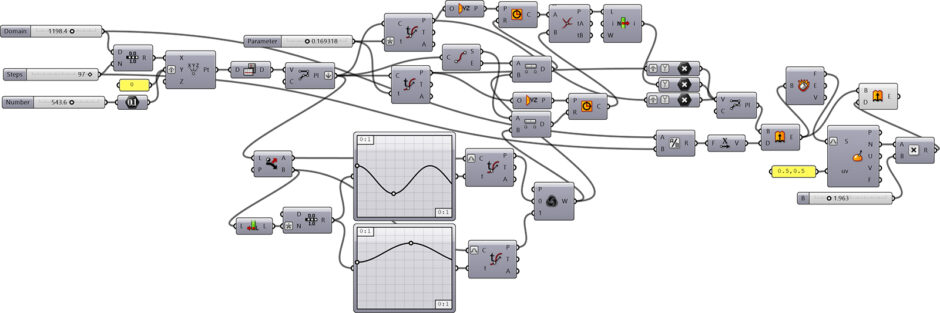 [4]
[4]You can rebuild the definition by looking at the diagram above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? The link to my Patreon page[5] includes the working Grasshopper file for the Contour-fold structure and more.

- here: https://www.designcoding.net/a-chord-folding-structure/
- here: https://www.designcoding.net/calatrava-door/
- Robert van Embricqs: https://www.robertvanembricqs.com/risingchair
- [Image]: https://www.designcoding.net/decoder/wp-content/uploads/2024/02/Contour-Fold-Structure-def.jpg
- The link to my Patreon page: https://www.patreon.com/posts/contour-fold-98049627?utm_medium=clipboard_copy&utm_source=copyLink&utm_campaign=postshare_creator&utm_content=join_link
Source URL: https://www.designcoding.net/contour-fold-structure/