Drawing and Unrolling Octahedron

by Tuğrul Yazar | December 29, 2011 11:37

An octahedron is a polyhedron[1] and platonic solid[2] with 8 faces of identical equilateral triangles. In this post, I will try to explain the drawing and unrolling process of the octahedron. It has a close relationship with the cube as it’s dual. In order to construct an octahedron, we first have to create a square. The main problem of drawing the square is determining the right angle (perpendicular axis) to any point in Euclidean space. We’ll draw it here as a two-dimensional projection. However, it can also be established in three dimensions using the same method (except for using spheres instead of circles). Start from any two points in the space;

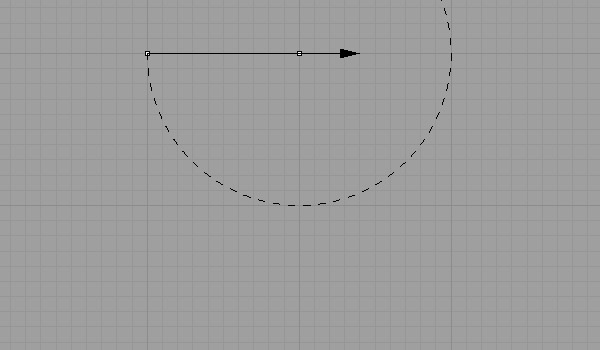
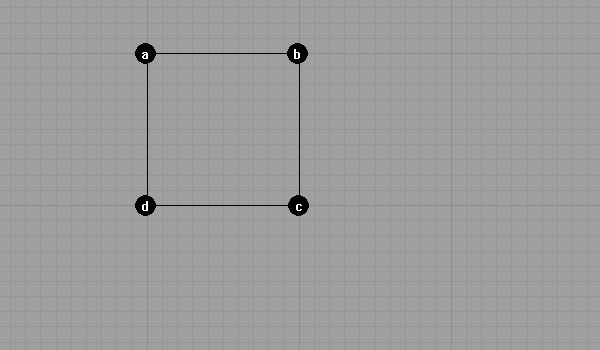
The Square

To create a right angle, we need to find a third point on the same axis and distance as the initial points. Using only a compass and ruler we establish that like this;

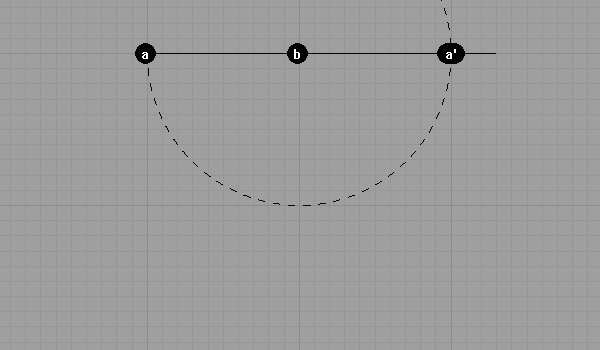
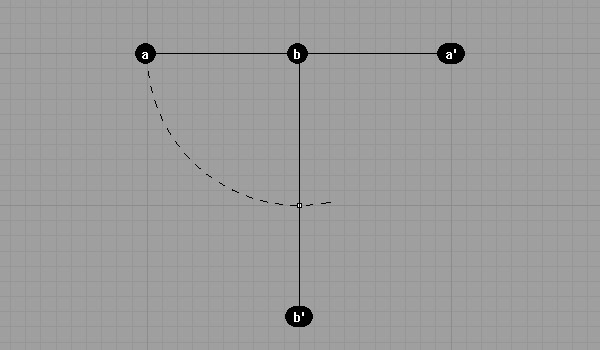
Now, we can find the perpendicular axis to point b, using points a and a’.

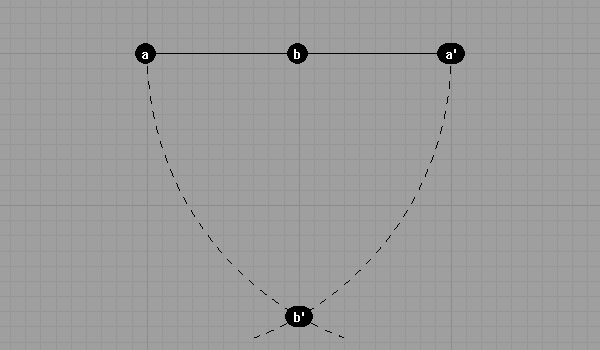
Drawing circles with center a and radius aa’, then center a’ and radius aa’. Found point b’ by intersecting these circles.

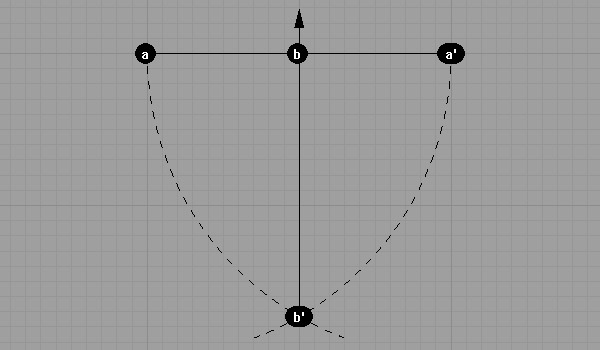
The line drawn using a ruler to connect b and b’ has to be perpendicular to line ab.

Rest is easier. Now, we can draw the square using this perpendicular. Intersecting the arc with center b and radius ab with line bb’.

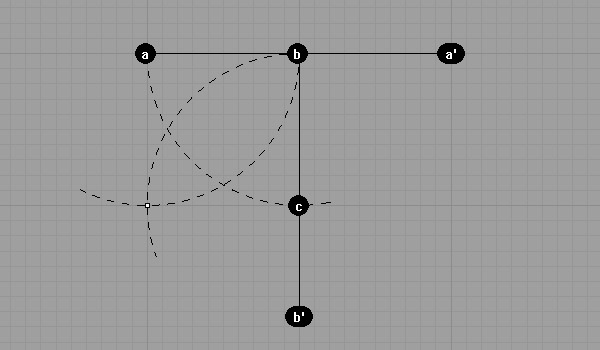
After finding point c, now use it to find point d.

Drawing the Octahedron

In order to construct a regular eight-sided solid, we’ll use a square as a basis.

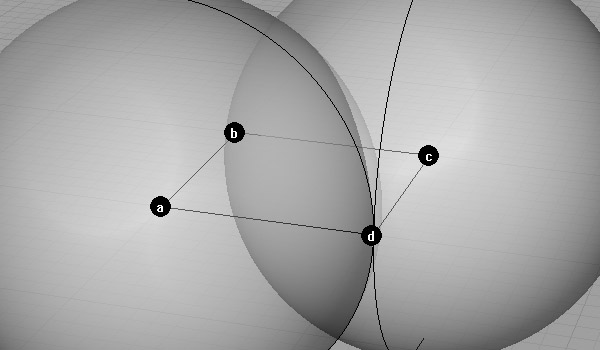
The problem is to find two points above and below this square, which lies at the same distance from all points a,b,c, and d. And the distance is the same as the edge of this square. Remember, we create the octahedron from eight equal and equilateral triangular surfaces. In order to find these points, we’ll intersect any three spheres from square corners with the radius of the square edge.

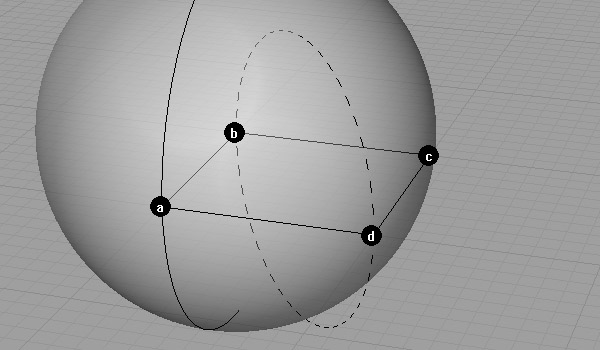
We intersected spheres a and c with radius ab. Found a circle. Thus, we need to intersect the third sphere to find points. This time it could be spheres centered at points b or d.

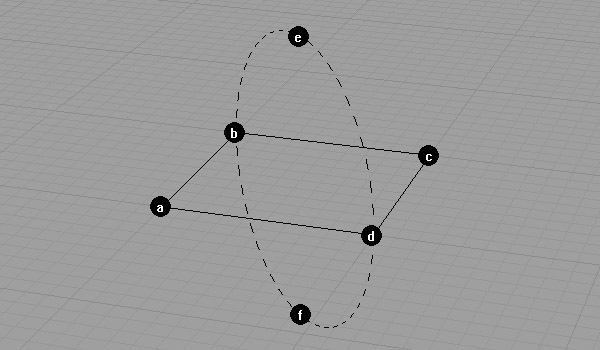
Then, after finding points e and f, the octahedron is almost finished.

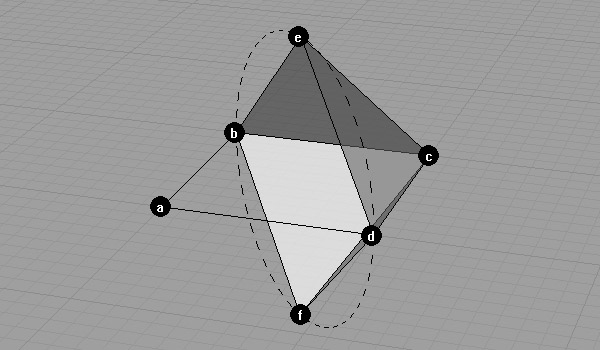
You may check the edge lengths of triangles if they are equal or not.

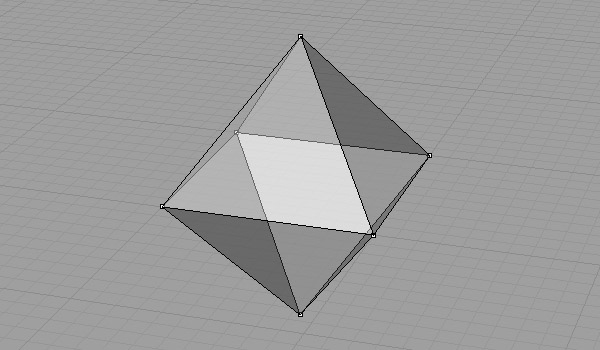
Unrolling the Octahedron

Octahedron has several unrolling sequences. I described one of them below. Note that the first step in this unrolling sequence creates another famous solid named “Rectified Tetrahedron”.

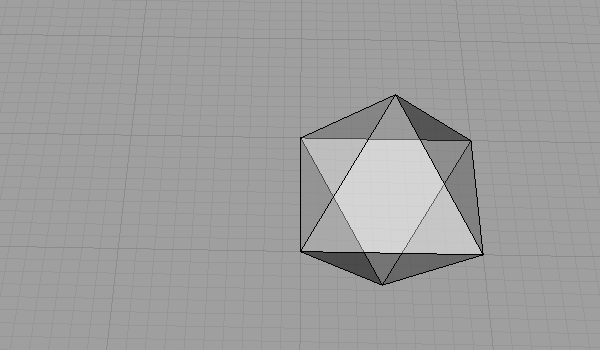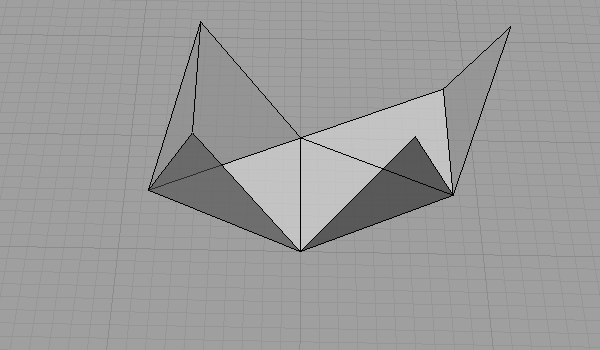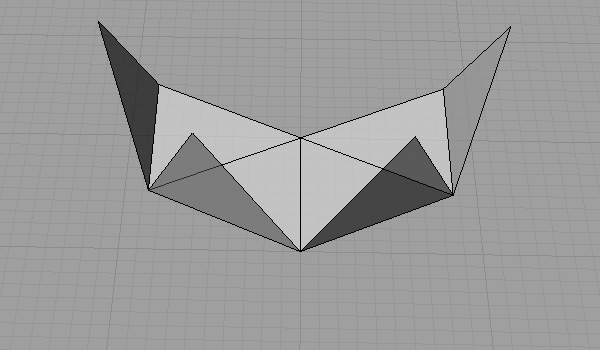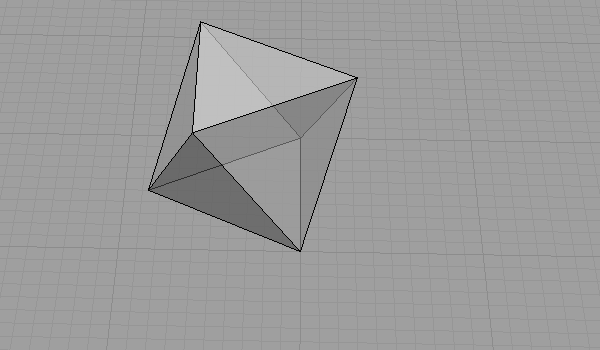
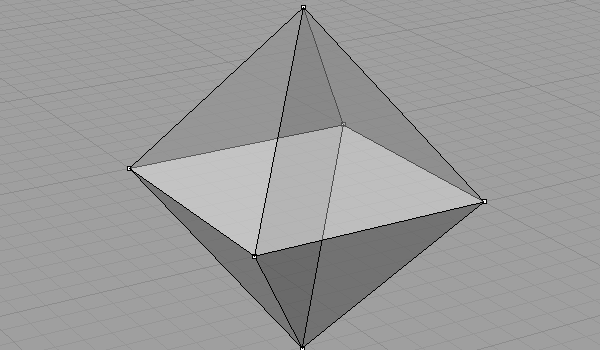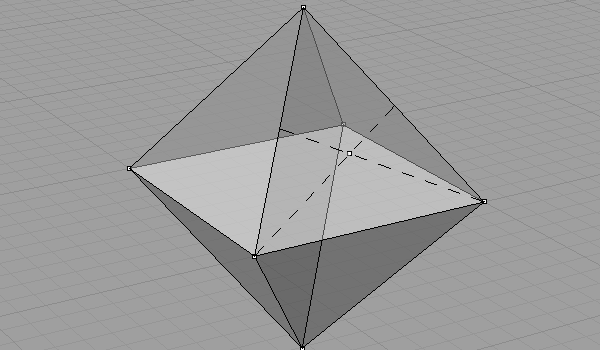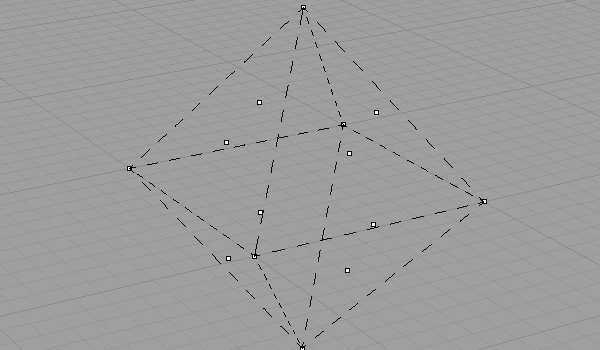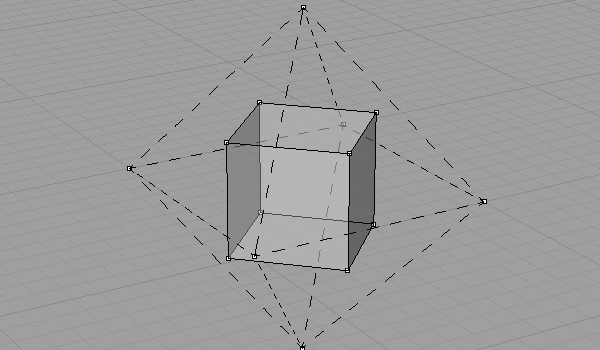
That was the drawing and unrolling of the octahedron. Cube is a dual octahedron as they have symmetrical vertex and face numbers. So, an octahedron has 8 faces and 6 vertices, and a cube has 6 faces and 8 vertices. This means, we may transform octahedron faces into cube vertices with the following method; Center points of all octahedron faces connect to construct a cube.

Source URL: https://www.designcoding.net/construction-and-unrolling-of-octahedron/

---