Constructing Tangent Circles
by Tuğrul Yazar | December 11, 2024 00:16
In geometry, “tangent” refers to a scenario where a line, curve, or surface touches another at exactly one point without crossing or leaving a gap. A tangent line to a circle is a straight line that touches the circle at only one point, and it is perpendicular to the radius at that point. Two circles can be tangent either internally or externally. Geometric constructions using a compass and straightedge can help accurately calculate tangent circles. Thus, the “constructing tangent circles” exercise aims at developing this reasoning through practical examples. Here, you can see several configurations of tangent circles and their radii. You will use compass constructions[1] to locate the center points of these circles and draw them. It is a good exercise for the geometric constructions.
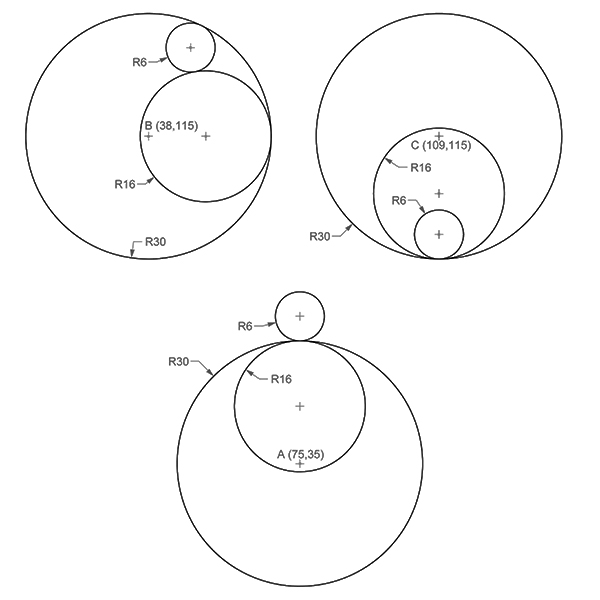
I have been conducting a series of in-class exercises in the freshmen year Architectural Geometry[2] course, focusing on Euclidean constructions, basic drawing and transformation commands, introductory fractals, regular and semi-regular tessellations, patterns, modeling, and unrolling polyhedra using Rhinoceros software. Junior architects, interior designers, industrial designers, and enthusiasts from other disciplines can benefit from these concise drawing exercises. I will publish exercises every week on my blog and other platforms. So, today’s exercise is: Constructing Tangent Circles.
The software used in this course is Rhinoceros 3d (www.rhino3d.com[3]). However, if you want to find out more and see the whole list of this video series, you can check my YouTube channel at www.youtube.com/@designcodingnet[4] and my blog at: www.designcoding.net/[5]. You can also check my Instagram page at www.instagram.com/designcodingnet/[6]. The music of this video is ‘The Long Dark’ by Scott Buckley (CC-BY 4.0). www.scottbuckley.com.au[7]
- compass constructions: https://www.designcoding.net/category/research/compass-constructions/
- Architectural Geometry: https://www.designcoding.net/category/education/design-geometry/
- www.rhino3d.com: http://www.rhino3d.com
- www.youtube.com/@designcodingnet: https://www.youtube.com/@designcodingnet
- www.designcoding.net/: https://www.designcoding.net/
- www.instagram.com/designcodingnet/: https://www.instagram.com/designcodingnet/
- www.scottbuckley.com.au: http://www.scottbuckley.com.au
Source URL: https://www.designcoding.net/constructing-tangent-circles/