Constructing Snub Square Tiling

by Tuğrul Yazar | December 11, 2024 20:41

Snub Square Tiling[1] is a semi-regular tessellation[2] of the plane, composed of two squares and three regular triangles at each vertex. The arrangement of these two regular shapes seamlessly covers the plane without any gaps or overlaps. It is one of the eight semi-regular tessellations known in geometry. The dual of Snub Square Tiling is Cairo Pentagonal Tiling[3], which we will explore later. In this short tutorial, I am drawing and constructing the Snub Square Tiling by using an abstract compass and ruler. The most interesting part of this construction is to draw the square tiles with only compass constructions[4]. I studied the same tiling here[5] and here[6] before.

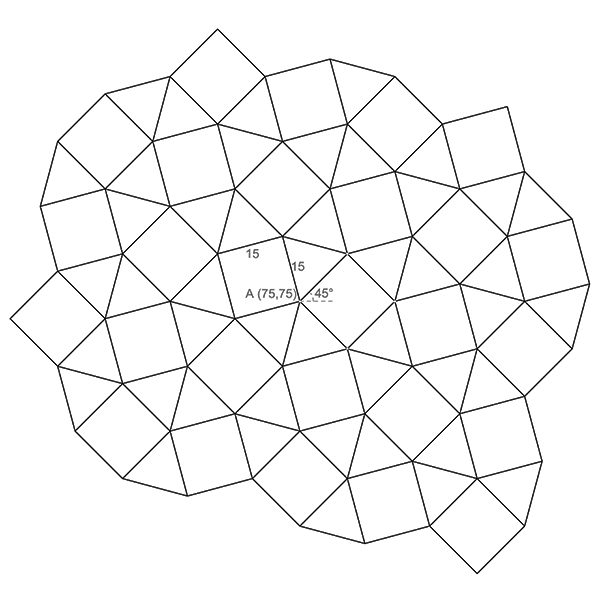
This video series showcases various in-class exercises I conducted in a freshman-year Architectural Geometry[7] course. Using Rhinoceros[8] software, we explore Euclidean constructions, basic drawing and transformation commands, fundamental fractals, regular and semi-regular tessellations, patterns, and modeling techniques, including unrolling polyhedra. These short drawing exercises are also beneficial for junior-level architects, interior designers, industrial designers, and enthusiasts from other disciplines. I will be publishing exercises each week on my blog and other platforms. Here is today’s exercise: Constructing Snub Square Tiling.

The software used in this course is Rhinoceros 3d (www.rhino3d.com[9]). However, if you want to find out more and see the whole list of this video series, you can check my YouTube channel at www.youtube.com/@designcodingnet[10] and my blog at: www.designcoding.net/[11]. You can also check my Instagram page at www.instagram.com/designcodingnet/[12]. The music of this video is ‘Artemis’ by Scott Buckley (CC-BY 4.0). www.scottbuckley.com.au[13]

Source URL: https://www.designcoding.net/constructing-snub-square-tiling/

---