Constructing Irregular Polygons

by Tuğrul Yazar | December 11, 2024 00:14

The geometric shapes constructed using only a compass and straightedge have significantly influenced the development of reasoning and logic that underpin modern science. This non-numerical approach is also known as the Synthetic Geometry. Before René Descartes introduced Analytic Geometry, this method was widely studied and practiced. In “Elements”, Euclid explores fundamental rules, such as ‘The straight line between two points is the shortest,’ and derives all geometric truths from simple, observable principles, built up step by step through logical deduction. In the “constructing irregular polygons” exercise, you will utilize compass constructions[1] to locate the points and draw the polygons. This basic reasoning behind such constructions is still valid for today’s computational design thinking.

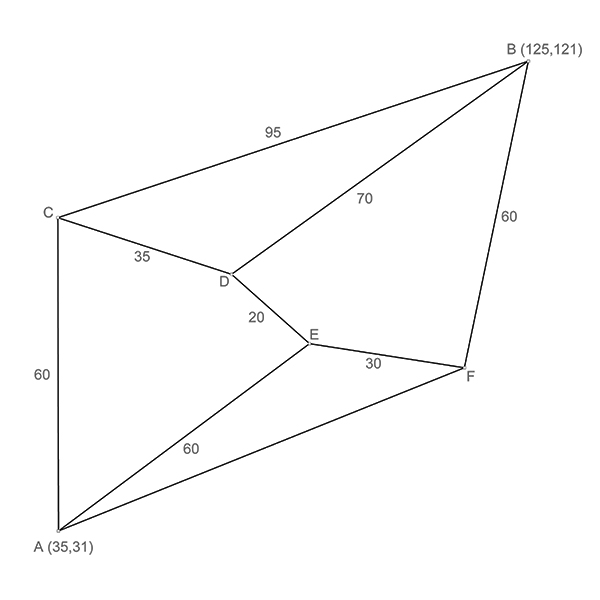
This video series showcases various in-class exercises I conducted in a freshman-year Architectural Geometry course. Using Rhinoceros software, we explore Euclidean constructions, basic drawing, and transformation commands. In addition, we will study some of the basic fractals, regular and semi-regular tessellations, patterns, and modeling techniques, including unrolling polyhedra. These short drawing exercises are also beneficial for junior-level architects, interior designers, industrial designers, and enthusiasts from other disciplines. I will be publishing exercises each week on my blog and other platforms. Here is today’s exercise: Constructing irregular polygons:

The software used in this course is Rhinoceros 3d (www.rhino3d.com[2]). However, if you want to find out more and see the whole list of this video series, you can check my YouTube channel at www.youtube.com/@designcodingnet[3] and my blog at: www.designcoding.net/[4]. You can also check my Instagram page at www.instagram.com/designcodingnet/[5]. The music of this video is ‘Cirrus’ by Scott Buckley (CC-BY 4.0). www.scottbuckley.com.au[6]

Source URL: https://www.designcoding.net/constructing-irregular-polygons/

---