After a couple of days of studying the mysterious Doyle spiral, I’ve decided to test an approach of circle packing from conformal mapping. First, I tried to understand the Poincare disk (earlier at here, here, and here and here). I used it as the hyperbolic representation of space on a two-dimensional plane. Then, I linked a regular hexagonal grid and rebuilt it after the hyperbolic distortion. This led me to find the below hexagonal grid. Therefore, it looks like a suitable foundation for a conformal circle packing:

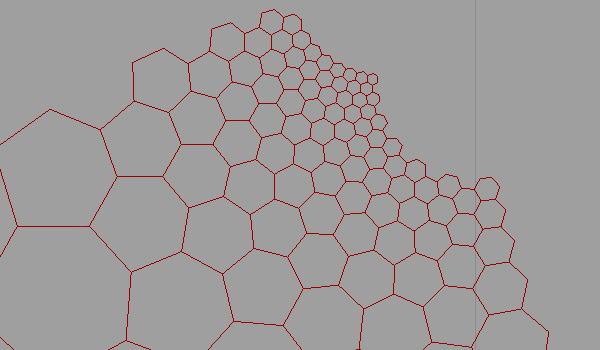
Looks like a Voronoi subdivision, but a very different thing in fact. My second attempt was to create a conformal circle packing out of this algorithm. However, I couldn’t manage to develop the Grasshopper algorithm perfectly. But in the end, the definition managed to create some circle compositions close to (but not exactly) a perfect packing:

You can download the Grasshopper definition of the above study here:

I developed the above Grasshopper definition in 2012. In 2021, it was still working as expected. Here is a small phrase, briefly explaining the idea of circle packing algorithms,

Circle packing as a discipline quickly attracted the interest of researchers in analysis, combinatorics, geometry, and topology, and initially developed along two not disparate branches. The one branch may be characterized broadly as analytic and combinatorial in style with particular attention focused on the relationship of circle packing to the approximation of conformal mappings. The other branch may be characterized broadly as geometric and topological in style with particular interest in the pure geometry of circle packing.

P.L. Bowers and K. Stephenson, Circle packings in surfaces of finite type: An in situ approach with applications to moduli, Topology 32 (1993), pp. 157