Compass only Construction of Bézier Curves

This is a new paper published in Nexus Network Journal. I tried to implement euclidean constructions by compass in the approximation of famous parametric curves; Bézier curves, and B-Splines. Then, I created the algorithms to calculate the number of steps on a compass-only construction of Bézier curves. I developed a simple Python script to simulate the geometric constructions. However, I have been studying this topic for nearly four years. In the future, I wish that it would be a good foundation for my further education.

This article reveals a mathematical bridge between compass-only geometric constructions and parametric curves. Therefore, a set of construction algorithms are presented. I used these algorithms to locate points on any Bézier curve or B-Spline by using an abstract compass. They aim to translate the B-Spline definition of Paul de Casteljau into the modified versions of compass-only constructions explained by Aleksandr Kostovskii. I developed several computer scripts to simulate these constructions while calculating and minimizing their computational complexities.

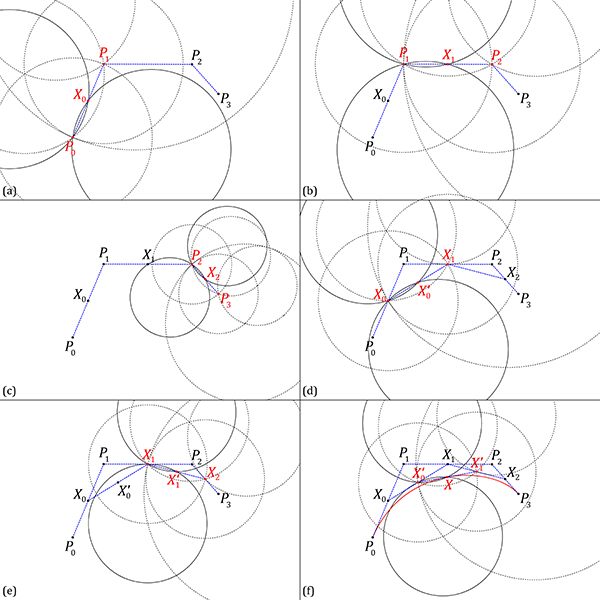
Compass construction of a point on a cubic Bézier curve (d=3, t=0.5). But, it is difficult to explain here. In short, I am using compass-only constructions to simulate the linear interpolation of two points.

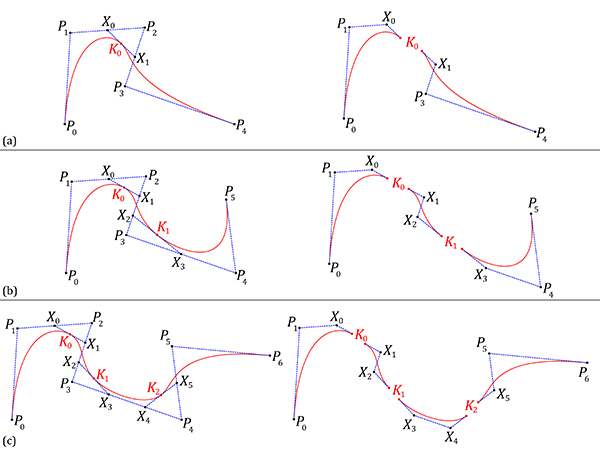
Compass-only de-construction pattern of several cubic B-Splines (d=3), locating their knots. Thus, it divides any given cubic B-Spline into its spans.

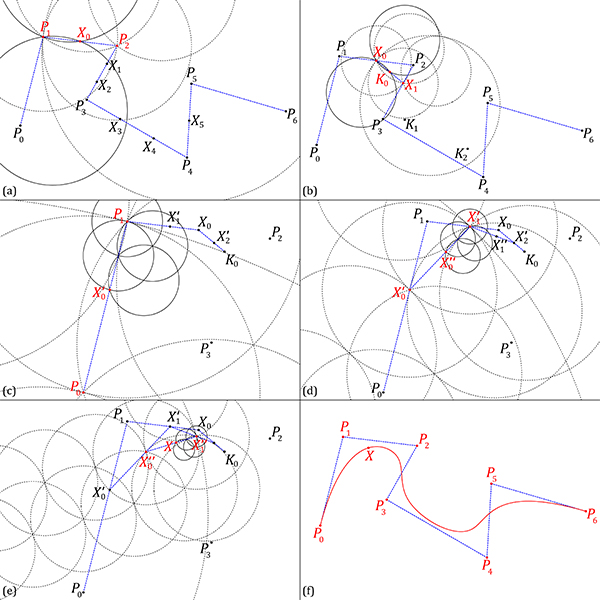
Calculation of the minimum number of compass operations required to construct a point at t = 0.6 on any span of a cubic B-Spline with seven control points (p=7, d=3).

You can find the full paper here. It explains the details and number of steps on a compass only construction of Bézier curves.