An Archimedean solid is a convex isogonal (vertex-transitive) and nonprismatic solid that is composed of two or more regular polygonal faces. There are thirteen such solids in geometry. Coding the snub dodecahedron study aims to generate one of these solids, composed of 12 regular pentagons, and 80 regular triangles. You can generate the snub dodecahedron by expanding and twisting the faces of a dodecahedron outward. This also creates rhombicosidodecahedron, which is another Archimedean solid. If you expand and twist the pentagonal faces out slightly less, then apply an equal rotation to the centers of the pentagons and triangles, continuing the rotation until the gaps can be filled by two equilateral triangles. This results in the snub dodecahedron. Another by-product of this code is the deltoidal hexacontahedron, a Catalan solid.

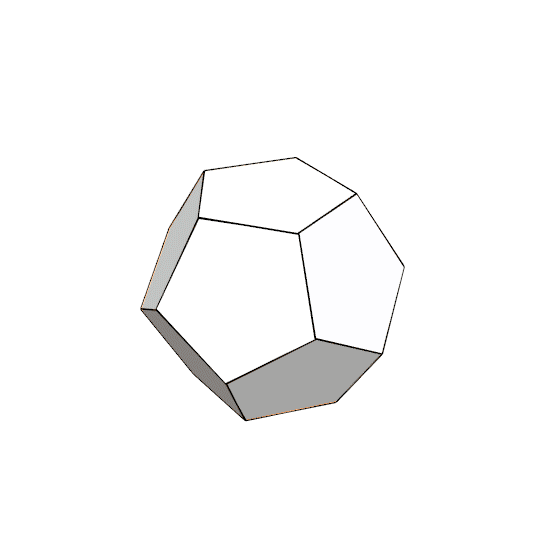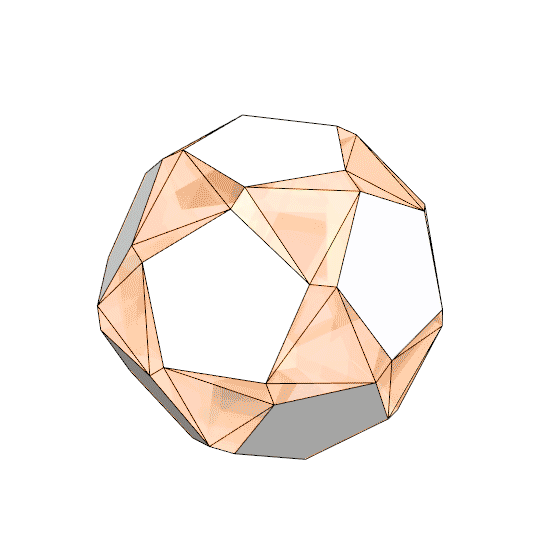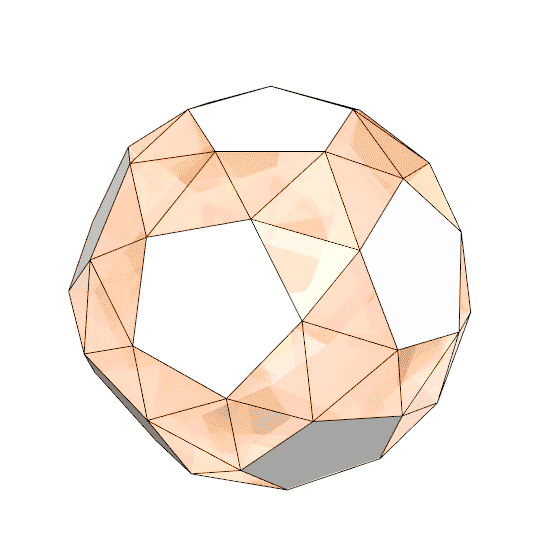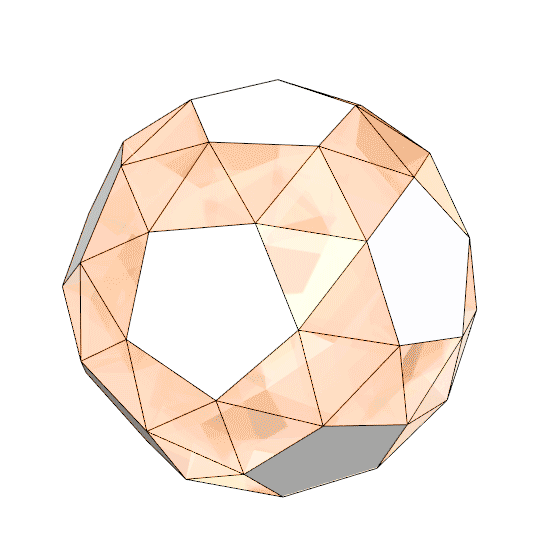
This Grasshopper definition generates several Archimedean and Catalan solids with geometric constructions. It is an educational and exploratory code to learn Grasshopper and generate interesting designs with it. The inputs of the definition control the expansion and twisting amounts of the initial dodecahedron. The output of the code is a closed polysurface of the resulting polyhedra. Therefore, it is ready for unrolling or 3d printing. The code is using native Grasshopper components. Thus, no add-ons are necessary for it to work.

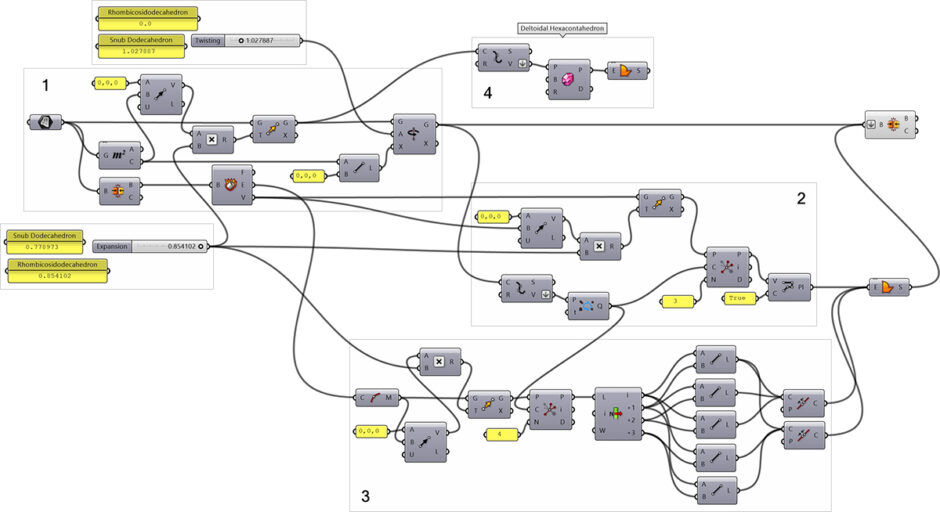
You can rebuild the definition by looking at the definition image. You need a dodecahedron as the starting model. If you liked this content, would you consider being my Patreon and downloading my Grasshopper file? Here is the link to my Patreon page, including the Coding the Snub Dodecahedron file and more. Thank you for your support.