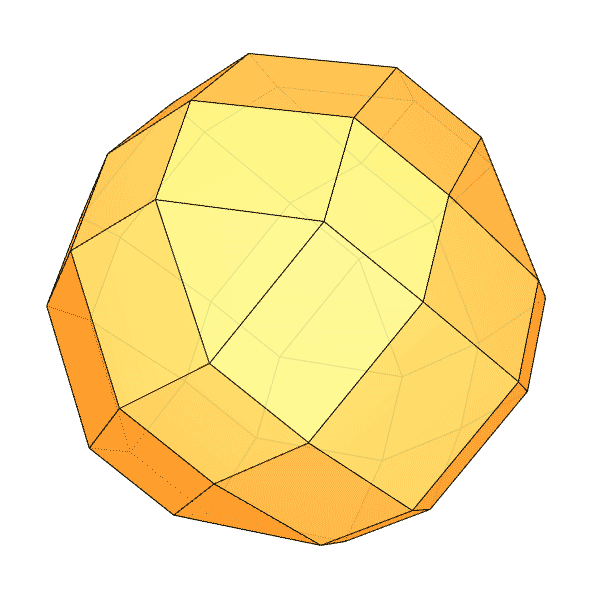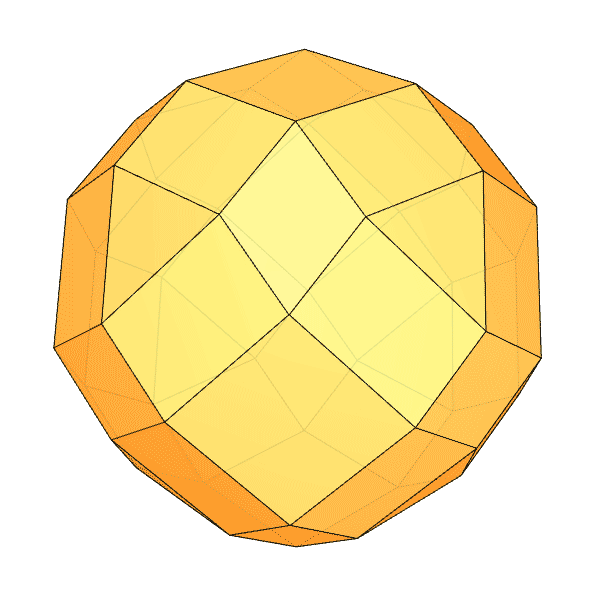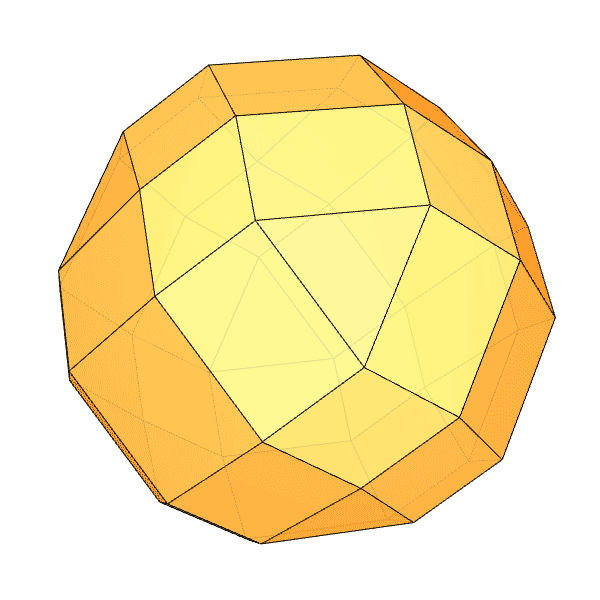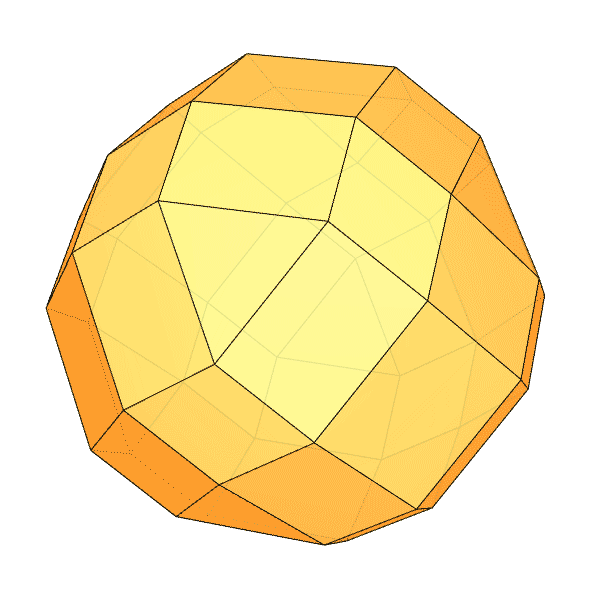
Chamfered Polyhedra
I had been researching Goldberg Polyhedra for a while. While exploring how to perform chamfer operations in Grasshopper, I found some interesting results. I want to share them with you. In this Grasshopper project, I reused my previous work, where I built a dodecahedron using the golden ratio. Essentially, all I did was add the Fillet Edge component. I don’t use this component much, so I learned it through this process. At one point, I realized I had created a Small Rhombicosidodecahedron. You can see my work on modeling the Archimedean solid in Rhino here. As I played with the parameters, I observed that many chamfered polyhedra emerged whose names I didn’t know. For example, when Factor=6.1892 and Radii=3.0, we get the shape you see at the bottom of this page. I named it “Augmented Rhombic Dodecahedron.” It has 12 rhombii, 12 squares, 8 triangles, and 24 rectangles.
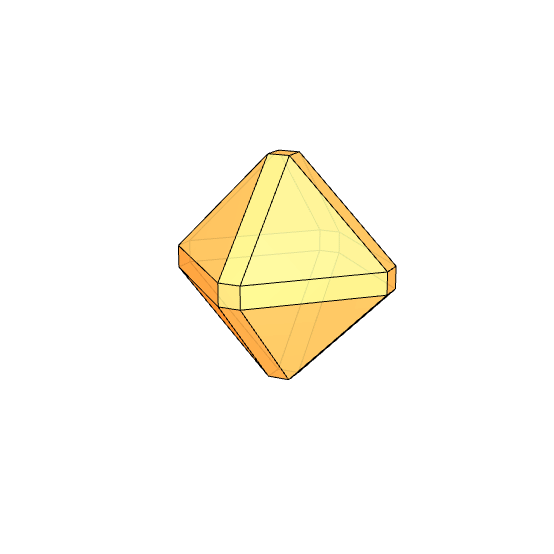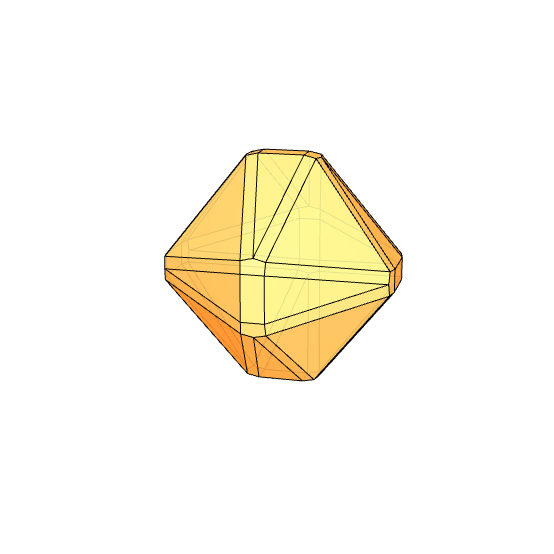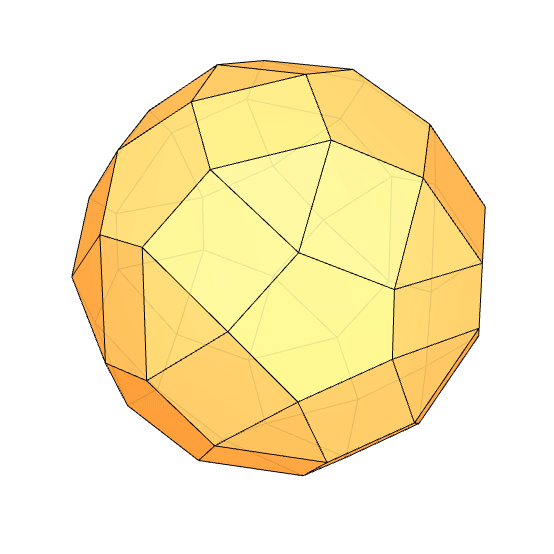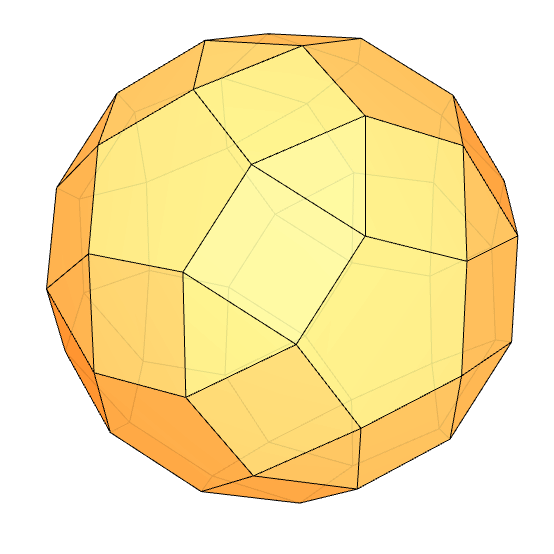
Like every polyhedron with rhombii, I found chamfered polyhedra quite appealing. I don’t know why these polyhedra are so attractive to me. Every time I think, “I’ve seen them all, they’re starting to get boring,” new ones appear. Nowadays, we are under a bombardment of high-curvature surface aesthetics. Polyhedra, on the other hand, are relatively simpler and more modest. They represent an older form of geometry. For me, these are transition spaces related to the design of mathematics. Beautiful symmetry games are completed in a spherical form that guarantees completeness and wholeness. They are inward-looking but beautiful.
Cite this post
Related Posts
Coding the Snub Dodecahedron
March 25, 2024
An Archimedean solid is a convex isogonal (vertex-transitive) and nonprismatic solid that is composed of two or more regular polygonal faces. There are thirteen such solids in geometry. Coding the snub dodecahedron study aims to generate one of these solids, composed of 12 regular pentagons, and 80 regular triangles. You can generate the snub dodecahedron by expanding and twisting the faces of a dodecahedron outward. This also creates rhombicosidodecahedron, which is another Archimedean solid. If you expand and twist the…
Space-filling Elongated Dodecahedra
February 22, 2024
The regular dodecahedron is one of the five Platonic solids, characterized by having 12 regular pentagonal faces, 20 vertices, and 30 edges. When you elongate it, you extend its structure in one or more directions, resulting in a shape that retains the basic properties of the dodecahedron but is stretched out. The elongated dodecahedron might not catch your eye at first—it’s just a long version of a shape you’ve probably seen before, and it seems pretty basic. But don’t be…
Space-filling Rhombic Dodecahedra
February 10, 2024
The rhombic dodecahedron is a polyhedron with twelve rhombus-shaped faces, where each face has four sides of equal length. It is possible to construct the space-filling variant of the rhombic dodecahedron by arranging multiple such rhombic dodecahedra in a regular pattern so that they fill space without leaving any gaps. In his 1611 work on snowflakes titled “Strena seu de Nive Sexangula,” Johannes Kepler observed that honey bees utilize the geometric structure of rhombic dodecahedra to construct honeycombs. These honeycombs…
Weaire-Phelan Space-filling Structure
December 20, 2023
The Weaire-Phelan structure is an optimal solution to the problem of partitioning space into equal volumes with the least surface area. Denis Weaire and Robert Phelan discovered it in 1993. This structure gained attention due to its efficiency in filling space, offering a configuration that achieves a more balanced distribution of volume and surface area compared to other known structures at the time. Here is my model for the Weaire-Phelan space-filling structure. The Weaire-Phelan structure consists of two different shapes:…
Coding the Dodecahedron
March 7, 2024
Here is a method for coding the dodecahedron and all its irregular variants in Grasshopper as quickly as possible. I utilized the golden ratio rectangles, usually used to construct the sister polyhedron, the icosahedron. However, the magic component of the Grasshopper, the Faceted Dome rescued me again to generate the dual of it, the dodecahedron. This is a special platonic solid, which has 12 regular pentagonal faces. There are several techniques that I generally prefer to use in Grasshopper. You…