In this study, I explore Cesaro Fractal, generated by Grasshopper. Usually, it is not possible to code recursive algorithms in Grasshopper. With the help of the Anemone add-on, these fractal curves are easy to model. I studied similar fractal algorithms here before. This one is very similar to the Koch’s snowflake. The only difference (as far as I understood) is the side of the spikes. Koch’s Snowflake generates triangular spikes pointing to the outside of the polygon. Cesaro Fractal does it pointing to inside. You can see some of the generations below. Therefore, the Grasshopper implementation is similar. One can modify this code to generate fractal-like shapes from any given polygon or polyline, not only the regular polygons.

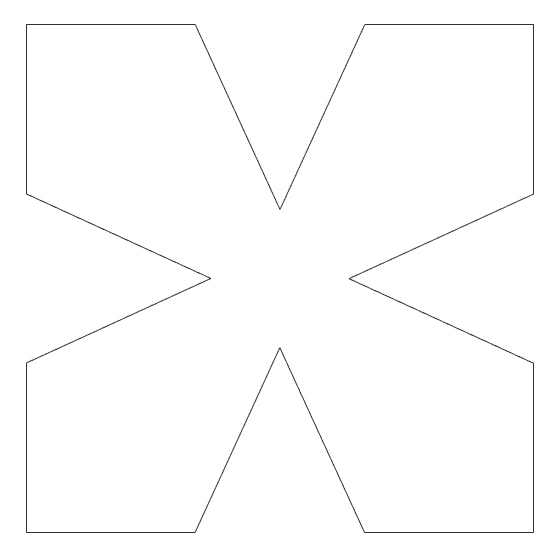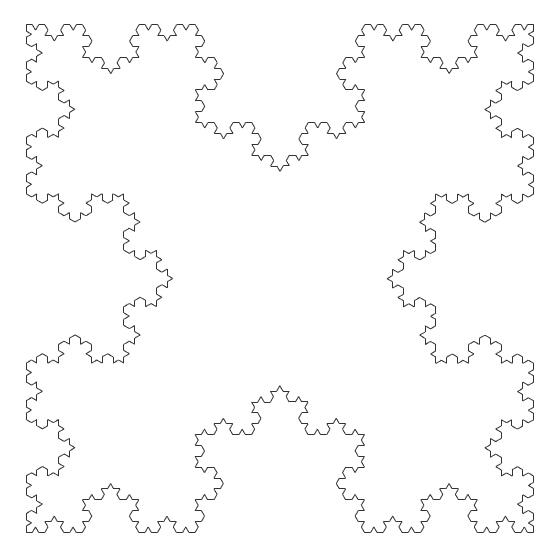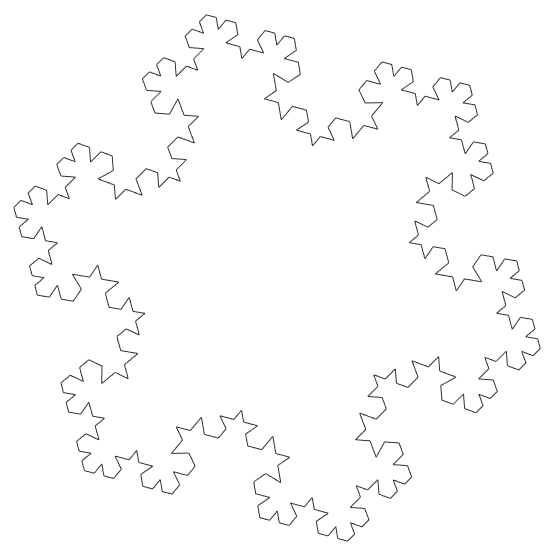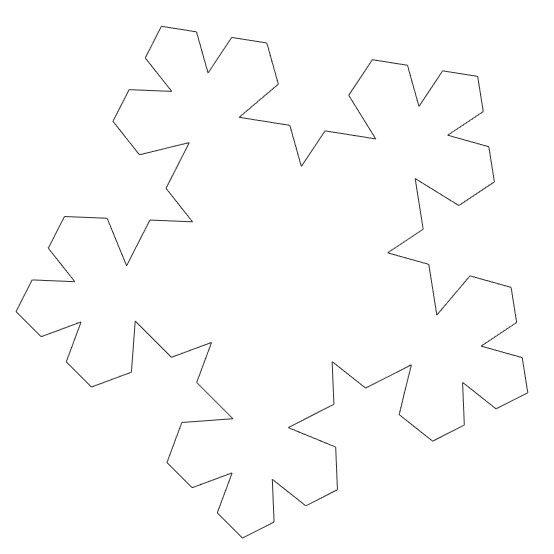
This Grasshopper definition generates Cesaro Fractal with several input parameters. The number of sides in the initial polygon, the symmetry and size of the spikes, and the number of iterations to process. It is possible to re-generate the classical Cesaro Fractal and also explore new designs as well. The resulting shape is a closed polyline. Therefore, it is ready for laser cutting. I made the definition with the help of the Anemone components in Rhinoceros 7. So, you need to install it from food4rhino first, to be able to use the definition.

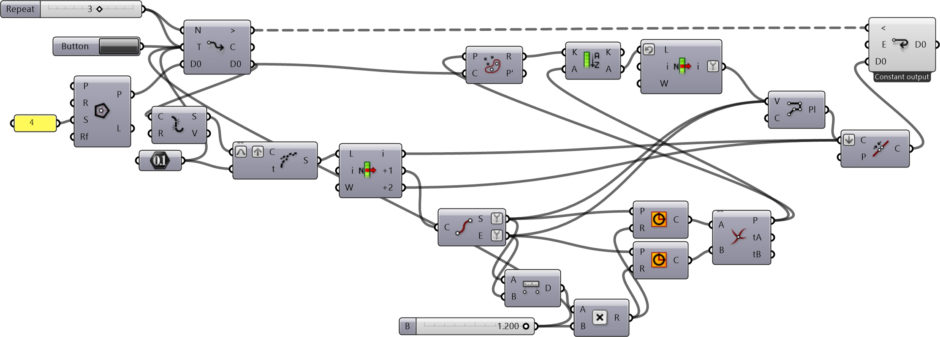
You can rebuild the definition by looking at the diagram above. However, if you want to support this website by downloading my Grasshopper file; would you consider being my Patreon? The link to my Patreon page includes the working Grasshopper file for the Cesaro Fractal and more.