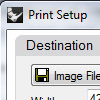
Here is a simple description of Rhinoceros’ Printing dialog. It is the same with version 4.0, nothing changed in layout and printing dialogs in 5.0. Significantly our Architectural Geometry classes should benefit from this explanation. Most of these options should be tested with a plotter (e.g. pencil widths) before final print-outs. Also, you may try creating a PDF file of your homework from this dialog.

I learned this method from the open math resources website. I couldn’t help myself repeat it in Rhinoceros. It was quite fun to solve circle tangency problems in 2D, this is one of them: drawing the circle that passes three given points, not using ready-made commands but only geometric tools of the circle (compass) and ruler (line). Here is the sequence of it: First of all, we need to know […]

Becoming popular after the Beijing 2008 Olympics National Aquatics Centre‘s facade (which is believed to be a Voronoi subdivision, as an epic mistake), the Weaire Phelan structure is a solution of equal volumes with minimal surface area. Although it is a structural solution, I think for architects, catching the eye with “cute bubbles” seems to be the primary purpose of this structure. (images from arup.com) A More Formal Explanation This […]

This elegant and straightforward tiling geometry is credited to Dominican priest Sebastien Truchet in 1704 and was documented in a book titled “Memoir sur les Combinasions” (A Memoir on Combinations). After delving into the renowned Truchet Patterns in 2013, I revisited their three-dimensional tiling counterparts today. This served as a valuable exercise in geometry during my previous Design Geometry course. I believe it enhances one’s proficiency in mastering the technical […]

Throne of my lonely niche, my wealth, my love, my moonlight.My most sincere friend, my confidant, my very existence, my Sultan, my one and only love.The most beautiful among the beautiful …My springtime, my merry-faced love, my daytime, my sweetheart, laughing leaf …My plants, my sweet, my rose, the one only who does not distress me in this room …My Istanbul, my karaman, the earth of my AnatoliaMy Badakhshan, my […]

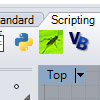
Last year, I posted a way to create a Grasshopper command button in Rhino 4 (here). As the scripting possibilities increase in Rhino 5, the new tab feature can be used to put them together. I’ve made 4 of the most used platforms in a tab named “Scripting”. Here is how I did it; Use right-click on the empty area to open the above menu and select “new tab” to […]

In this exercise, we asked students to develop a method to produce custom tessellations. This is based on the analysis of what is called “Islamic patterns”. We have discussed Eric Brough‘s famous book “Islamic Geometric Patterns”, regarding geometric relationships and linear connectivities via underlying tessellations (such as regular square and hexagonal). Thus, this geometry and drawing exercise is called “Seamless Patterns” in the Design Geometry course at İstanbul Bilgi University. […]

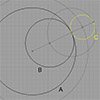
The first-year Architectural Geometry course includes Euclidean constructions as a study of associative geometry. We have exercised the below questions to study this topic. These are three mutually tangent circles, that can be drawn using only a compass and ruler, without built-in tangency functions in Rhino. Such exercises are expected to improve students’ reasoning. We believe architectural geometry education should encourage a conception that allows students to think about what […]

This is not to explain the method of the Parquet Deformation but to see the potential. After we’ve studied regular, semi-regular, dual, and truncated tessellations with students, the Architectural Geometry course expects them to develop a Parquet Deformation handmade such as those shown below. I call them Parquet Deformation handmade. Because they are manually designed but drawn using traditional CAD. The samples you see below are from this website. It […]

The poincare disk is still an interesting representation of hyperbolic space for me, full of mysteries. I’ve had several attempts to understand it previously (here and here). Finally, I found a resource* explaining basic concepts about it. I tried to repeat some of the constructions in Rhinoceros, (without any logical purpose). The most important part is the conversion of a Euclidean point into a hyperbolic space. There is no clear […]

The Truncated Icosahedron (5,6,6) is an Archimedean Solid we often recognize as the iconic soccer ball. This geometric structure, also affectionately known as the “Buckyball” in honor of the visionary architect Buckminster Fuller, has gained significant popularity and recognition both within the realms of mathematics and everyday life. It is composed of twelve regular pentagons and twenty regular hexagons, meticulously arranged to achieve a harmonious balance. This symmetrical nature makes […]

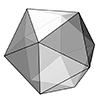
Not all of them, but when you get the idea, you’ll see there are lots of different alternatives for creating Fuller’s famous Geodesic Domes (Although in fact, he is not the inventor of it). I was playing with Platonic Solids in Rhino and realized that the “Pull” command is very useful in subdividing objects. I modeled this in Rhino 4. First, take a regular Icosahedron and divide it. Because, this […]

The tetrahedron is a popular platonic solid for designers. We’ve explained how to draw them using equilateral triangles here before. Recently I’ve found (sorry, lost the web address) a much quicker way of modeling a Tetrahedron using a cube. It’s very simple, just connecting the three opposite corners of the cube automatically makes them equal, resulting in the four equal faces. Of course this time you’ll have to calculate the […]

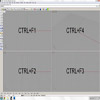
Here are three technical tips, that might help you model in Rhinoceros faster. Please note that, in most cases, you’ll find CTRL+F1,F2,F3 and F4 very helpful in modeling and transforming objects in digital space. These key combinations will focus you on Top, Front, Left and Perspective views (maximized) respectively. Also, when you try to express your design process (especially supporting geometries) using different linetypes, it’s possible that you’ll never like those preset linetypes. By […]

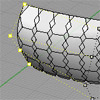
The cellular canopy is an anonymous tutorial on the history recording capability of Rhino. I’ve been using a “pedagogical” version of this tutorial as an educational tool on the introduction to Grasshopper and Parametric Modeling for architects. The interesting thing with such exercises is they quickly attract students’ attention to the process of designing, in other words, “designing the design process”; is one of the first things we should emphasize […]

An octahedron is a polyhedron and platonic solid with 8 faces of identical equilateral triangles. In this post, I will try to explain the drawing and unrolling process of the octahedron. It has a close relationship with the cube as it’s dual. In order to construct an octahedron, we first have to create a square. The main problem of drawing the square is determining the right angle (perpendicular axis) to […]

Recording History in Rhinoceros3D has interesting potential. You might utilize it in the process of design exploration. We’ll try to show its concept and limitations; First, build two surfaces; one is planar at the world XY plane, and the other represents the “initial” form of your design. Put another surface on the planar one, as if it’s an ideal “component” of the finished geometric composition. Activate the “Record History” button […]

Icosidodecahedron is an Archimedian Solid, a thing in between the Platonic Solids of Icosahedron (d20) and Dodecahedron (d12). It is a rectified version of an Icosahedron, constructed by dividing every edge into two equal segments and joining these segments to create a composition of equilateral pentagons and triangles. Archimedian Solids consist of at least two equilateral polygons, whereas Platonic Solids are constructed by only one. We’ll deduce an Icosidodecahedron from […]

Today’s polyhedra is the beautiful icosahedron. It is one of the five Platonic Solids with twenty equilateral triangular faces. Its dual is the dodecahedron, which has pentagonal faces. Here, I explained the process of modeling an icosahedron. After creating a regular pentagon, you should find the “tip” point of the Icosahedron by intersecting spheres from at least three of the corner points with a radius of the pentagon’s edges. You […]

A truncated Tetrahedron is an Archimedian Solid, created by slicing a Tetrahedron. Its faces are regular hexagons and triangles. Assuming you’ve created a Tetrahedron, first join its faces to create a polysurface. Now, you may re-create the lines of Tetrahedron’s edges, either by drawing them or generating them (Curve/Curve from Objects/Duplicate Edge). While the edge lines are selected, hit (Curve/Point Object/Divide Curve By/Number of Segments) and type 3 to create the […]